Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 34
Determine o limite infinito.
Passo 1
Eaee, belezinha?? Bom... a questão quer que determinemos o seguinte limite infinito:
Lembrando que a cotangente é dada pela razão do cosseno pelo seno (que é o inverso da tangente).
Em outras palavras, podemos reescrever os eguinte limite:
Em outras palavras, a questão nos diz que esse limite é infinito, ou seja, ele diverge. Mas queremos saber se irá divergir para ou .
Para isso, temos que aplicar o no numerador e no denominador para verificarmos se estes apresentarão resultados positivos ou negativos.
Agora bora colocar isso em prática!! 😉
Passo 2
Aplicando primeiramente ao numerador, temos que:
Ou seja, o numerador tenderá para um número negativo. Aqui, o fato de pelos números à esquerda não faz diferença no resultado.
E para o denominador temos que:
Aqui, o fato de pelos números à esquerda faz diferença no resultado.
Perceba que se fizermos um número ligeiramente menor do que , o seno tenderá a zero pelos números positivos. Veja a seta verde no círculo trigonométrico da função seno:
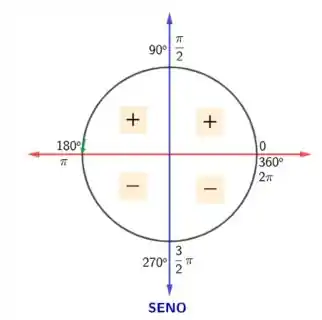
Assim, resultaremos em um número positivo próximo de zero.
Portanto, o denominador é um valor positivo que se aproxima de . Assim, temos que:
Passo 3
Aplicando a propriedade do produto para o limite, obtemos por fim que: