Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 15q
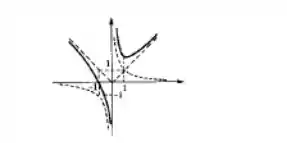
Dê o domínio e esboce o gráfico.
Passo 1
O domínio dessa função é bem tranquilo. Lembrando que não podemos ter divisão por zero, então:
Tranquilo?
Passo 2
Agora o esboço do gráfico. Ele vai ter cara de hipérbole, porém com aquele o desenho fica um pouco diferente.
As raízes dessa função serão:
Encontramos apenas um valor de que soluciona essa quação:. E ela não corta o eixo , pois .
Agora aos limites:
- Quando o termo tende a zero, então o comportamendo dominante é do . Sendo assim, quando o gráfico tende a .
- Quando , tanto pela direita, quanto pela esquerda, o termo dominante agora é . E o gráfico, em torno da origem, toma o comportamento da hipérbole que tende a , quando se aproxima de zero pela direita e tende a , quando se aproxima pela esquerda.
Show! Agora vamos juntar todas essas informações e construir o esboço! Bora lá?
Passo 3
Juntando todas essas informações e com a ajuda de um programa de geração de gráficos temos o esboço:
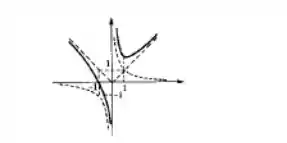
Os esboços de e de estão pontilhados. A linha cheia é o resultado da soma dessas duas funções. Quando , esse esboço tem a cara da função modular. Agora quando olhamos em torno da origem, ela se parece mais com a hipérbole.
Ok?
Vamos pra próxima?
Resposta
