A eletricidade é fornecida para as casas na forma de corrente alternada, significando que a voltagem tem uma forma senoidal, descrita por uma equação da forma
(ver figura abaixo). Nessa equação, é o pico de voltagem ou amplitude da corrente, é a frequência e é o período. As voltagens e são medidas em volts (), o tempo é medido em segundos () e a frequência é medida em hertz () (ciclo por segundo; um ciclo é o termo elétrico para um período.) Os voltímetros de corrente alternada medem o que é chamado rms ou raiz média quadrada do valor de . Por definição, isso é a raiz quadrada do valor médio de sobre um período.
(a) Mostre que
[Sugestão: Calcule a média sobre o ciclo de a , e use a identidade para ajudar a calcular a integral.]
(b) Nos Estados Unidos, o fornecimento de energia elétrica é feito com uma voltagem rms de , a uma frequência de . Qual é o pico de voltagem desse fornecimento?
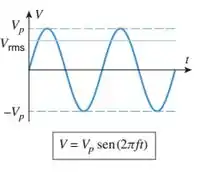
Passo 1
(a) O enunciado diz que a definição de é a raiz quadrada do valor médio de sobre um período, ou seja no intervalo de tempo de . A gente pode usar a sugestão do enunciado e essa definição para calcular :
A fórmulinha para o valor médio de uma função é em um intervalo é:
Para a função no intervalo essa fórmula do valor médio fica assim:
Vamos calcular essa integral e achar . Vem comigo!
Passo 2
Vamos reescrever nossa integral:
Podemos usar a identidade que o enunciado sugere para reescrever esse integrando aí:
Usando a substituição :
Passo 3
Agora é só lembrar que:
Uhul! Conseguimos!
Passo 4
(b) A gente acabou de ver que o pico de voltagem se relaciona com , e isso independe da frequência. A gente só precisa usar essa relação:
O enunciado diz que . Então:
Resposta
(a) Prova nos passos
(b)