Encontrar as derivadas laterais das seguintes funções, nos pontos indicados. Encontrar os intervalos onde e .
Passo 1
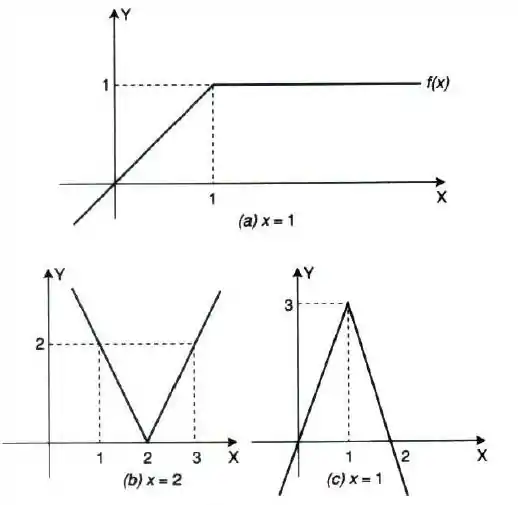
Pessoal, na letra (c) temos a seguinte função:
Vamos agora calcular as derivadas laterais! Se a função está definida em , então as derivadas à direita e a esquerda de em , denotadas por e são definidas por:
Bora começar!
Passo 2
Uma função é derivável em um ponto, quando as derivadas à direita e à esquerda nesse ponto existem e são iguais. Assim, temos:
Assim, temos que
Portanto, é crescente em e negativa e decrescente em .
Resposta
é crescente em e negativa e decrescente em .