Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 4
Encontre a área da região sombreada:
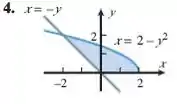
Passo 1
Para calcularmos a área entre as curvas vamos calcular a integral fazendo a diferença entre as funções de cima e debaixo, no entanto, nesse caso, como x varia entre funções, e y entre constantes, fazemos a integral em relação a y ao invés de x como estamos mais habituados.
Observa que y varia desde y=0 até o ponto onde as funções se encontram.
O y que nós prcuramos é positivo, por isso:
Opa, sabemos então que as funções se encontram no y=2. Queremos então saber a área entre y=0 e y=2.
Passo 2
Calculando isso temos:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região entre a curva y = sec 2 x , - π 4 ≤ x ≤ π 4 , e o eixo x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região limitada pela parábola y = x - x 2 e pela reta y = - x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região no primeiro e quarto quadrantes, delimitadas pelas curvas y = 1 1 + x 2 e
16- Determine o centro de massa de uma placa fina que abrange a região limitada abaixo pela parábola y = x 2 e acima pela reta y = x , se a densidade da placa no ponto ( x , y ) for δ x = 12 x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada. A região limitada pelas parábolas y = 2 x 2 - 4 x e y = 2 x - x 2 .