Encontre as assíntotas horizontais e verticais.
Passo 1
Olá, meu amigo. Aqui a questão nos pede para que a gente encontre as assíntotas verticais e horizontais da função dada.
Para encontrar a assíntota horizontal de uma função, tomaremos o limite da função quando .
Já para encontrarmos a assíntota vertical é muito simples e você vai ver, devemos pensar o seguinte “Para que ponto que quando se aproxima a função ‘explode’ para infinito”.
Como na nossa função temos uma divisão, isso vai ocorrer quando estivermos próximo de dividir por zero.
Passo 2
Para a assíntota vertical, precisamos encontrar tal que:
Para a condição de assíntota é satisfeita, pois quando mais próximo de é o denominador, maior será o numerador, ou seja, ocorre quando , logo é uma assíntota vertical.
Note que os valores de são calculados igualando o denominador a e encontrando os valores de .
Passo 3
Já para a assíntota horizontal, faremos:
Nesse limite, devemos colocar o de maior potência do denominador e do numerador em evidência:
Dessa forma, podemos cortar
E quando tende a infinito, temos que tende a zero, logo:
Portanto, temos uma assíntota horizontal em .
Passo 4
Mostraremos agora uma comprovação gráfica do resultado obtido
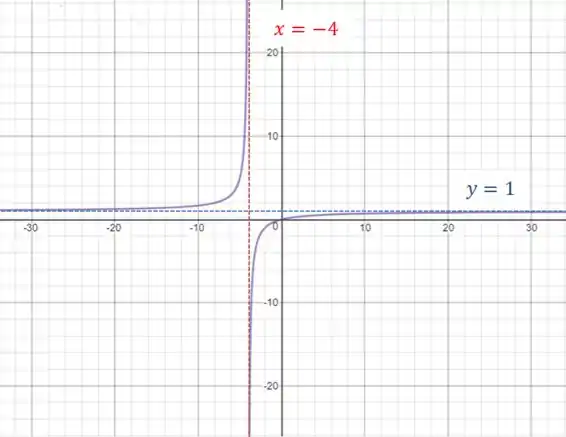
Resposta
é uma assíntota horizontal.
é uma assíntota vertical.