Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.6 - Ex. 42

Encontre as assíntotas horizontal e vertical de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.

Passo 1

Olá, meu amigo. Pronto para mais uma resolução?

Aqui a gente tem a função:

E devemos encontrar suas assíntotas verticais e horizontais. Além disso, iremos plotar o seu gráfico para conferir se nosso trabalho foi bem feito.

Antes de darmos início vamos ao resumo sobre as assíntotas.

Assíntotas Verticais: As assíntotas verticais ocorrem quando a função se aproxima de um determinado valor de , mas nunca o alcança. Elas são encontradas onde o denominador da função se torna zero, mas o numerador não. De modo geral, as assíntotas verticais ocorrem em pontos que levam o limite da nossa função ao infinito, em pontos onde nossa função não está definid.

2. Assíntotas Horizontais: As assíntotas horizontais ocorrem quando a função se aproxima de um determinado valor de , à medida que se aproxima do infinito ou menos infinito. Para determinar as assíntotas horizontais, você precisa verificar o comportamento da função quando se torna muito grande (positivo ou negativo). Se a função se aproxima de um valor específico de à medida que se torna muito grande (positivo ou negativo), então há uma assíntota horizontal nesse valor de .

Lembre-se de que nem todas as funções têm assíntotas verticais ou horizontais. Então é isso, vamos analisar os limites da nossa função e a partir deles é que iremos encontrar as assíntotas.

Passo 2

Começaremos com a assíntota horizontal, temos que fazer:

Se der um número real, a assíntota será esse número. Caso dê infinito não teremos assíntota horizontal. Vamos para o cálculo!

Como o limite aqui vai para infinito, vamos simplificar de forma a termos e esses termos serem zerados no calculo do limite:

Tirando o de dentro da raiz, lembrando o que fica fora é o módulo.

Sabendo que para .

E que para .

Voltando para a expressão:

Reduzindo os dois e colocando o limite em todas as parcelas, temos:

Calculando individualmente cada limite:

Substituindo tudo para dentro do limite, temos isso aqui:

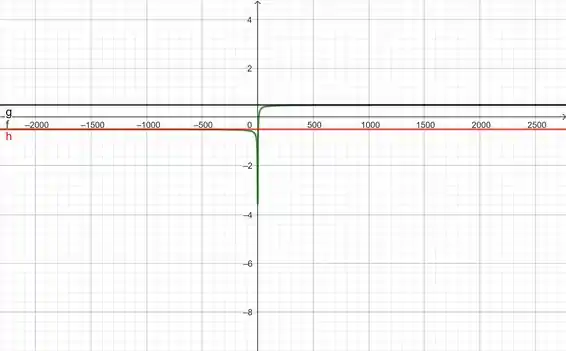
Então, temos assíntota horizontal para positivo e é a reta

Passo 3

Agora para :

Sabendo que para

Voltando para a expressão, temos:

Reduzindo os dois e colocando o limite em todas as parcelas, temos:

Substituindo tudo para dentro do limite, temos isso aqui:

Então, temos assíntota horizontal para negativo e é a reta .

Resumindo, quando estivermos caminhando para valores absurdamente grandes de , teremos uma assíntota em mas quando estiver caminhando para valores absurdamente grandes de teremos uma assíntota em

Passo 4

Lembra como fazemos as assíntotas verticais?

Os candidatos a assíntotas verticais são os pontos em que a função não está definida.

Para vermos se há algum ponto que não existe, temos que anular o denominador ou torná-lo negativo.

Isso significa que a nossa função não possui zeros, e por seu termo ela também é positiva para todos os números reais. Sendo assim, não temos pontos de indeterminação nessa função e ela não possui assíntotas verticais.

Vamos então plotar o gráfico com ajuda do GeoGebra e ver se estamos certos.