Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.9 - Ex. 22
Encontre uma representação em série de potências para , trace e várias somas parciais na mesma tela. O que acontece quando aumenta?
Passo 1
Olá pessoal, tudo bem?!
Vamos resolver este problema passo a passo.
Primeiro, nosso objetivo é encontrar uma representação em série de potências para a função . A função envolve o algoritmo natural de uma expressão quadrática. Uma abordagem comum para encontrar a série de potências de uma função é manipular essa função para que ela se assemelhe a uma série de potências conhecida, como , e então integrá-la termo a termo. Essa série de potências é conhecida e derivada da série geométrica. Sua representação é dada por:
Passo 2
Para encontrar a série de potências para , começamos considerando a função . Primeiro, vamos reescrever a função de logaritmo em termos de uma integral:
Vamos manipular a fração para que ela se assemelhe à forma , que é a série geométrica:
Aplicando a definição de série geométrica na nossa função:
Como é constante, podemos tirá-los do somatório:
Passo 3
Agora, podemos integrar termo a termo:
Como a integral de uma soma é a soma de integrais, podemos escrever:
Calculando a integral de cada termo:
Somando as integrais:
Para determinar a constante de integração , vamos considerar :
Portanto, a série fica:
Passo 4
Beleza! Agora, não faz diferença se trocarmos por na equação acima, e assim descobriremos a expressão para :
Passo 5
Show! Agora vamos traçar e primeiras somas parciais a partir da série de potências encontrada no passo anterior.
As primeiras somas parciais são:
Traçando os gráficos da função :
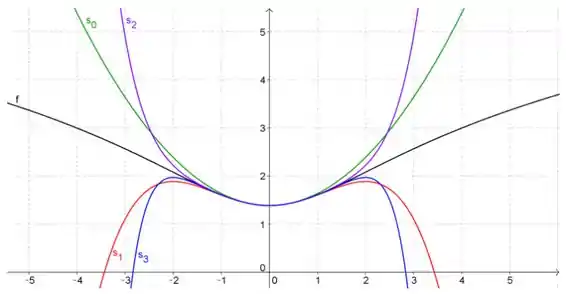
Perceba que, à medida que aumenta, as somas parciais se aproximam cada vez mais de no intervalo de convergência, ou seja, quando . As somas parciais fornecem aproximações cada vez melhores da função dentro desse intervalo.