Encontre todos os pontos onde não é diferenciável. Justifique sua resposta.

(a)

Para uma função ser contínua em um ponto :

Se isso acontecer, é contínua em .

Então, queremos um ponto em que a função não seja contínua. Mas são tantos ponto possíveis, qual posso testar?

Se liga aqui, vou te dar uma dica nessas horas:

Vamos pensar numa parábola . Seu gráfico é:

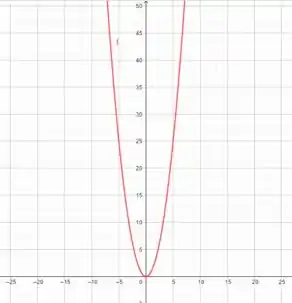
E se a gente der um zoom maneiro em algum ponto desse gráfico, vamos ter algo:

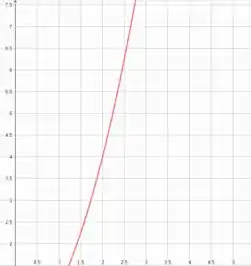
Repare que quanto maior o zoom que nós damos, a parábola se parece cada vez mais perto de uma reta.

Agora, vamos olhar para essa função módulo que temos no problema, . Seu gráfico é:

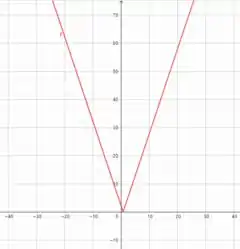
Vemos duas retas, que se dermos zoom, vamos continuar vendo retas. Mas e esse vértice em ? Se a gente der um zoom nele, muda alguma coisa? Vamos ver:

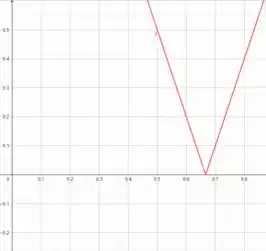
Cara, o gráfico continua com aquela cara de triângulo invertido, certo? Esse ponto é um forte candidato pra gente, então!!

Aí você pode se perguntar sobre o vértice da parábola, a grande dica é: a parábola possui uma curva naquele local, o que dá um comportamento “diferenciável”, digamos assim, isso porque curvas possuem derivadas (pelo menos a princípio). A função módulo tem um ponto ali, rodeado de retas. As retas possuem uma derivada, só olhar para equação da reta , se você deriva, acha , então qualquer reta tem uma derivada (pelo menos a princípio). Agora, nesse vértice do módulo, temos um ponto. “Pontos não são deriváveis”, isso porque ao derivar uma forma, você diminui a dimensão dela e o ponto já é a menor dimensão possível (dimensão 0). Beleza?

Conclusão: vamos tester o ponto , porque ele está no vértice desse módulo.

Calculando o limite:

Onde:

Ou seja, ela é definida por:

Vamos olhar para os limites laterais e eles devem coincidir.

Limite lateral pela esquerda:

Limite lateral pela direita:

Opa, os limites laterais coincidiram, então:

Para a função ser contínua em :

Como vimos:

Agora, olhando para a função:

Quando , a função vale obedece essa equação: . Então:

Muito bom! Dessa forma, é contínua em , já que:

Agora, falta só ver se existe.

Vamos calcular o limite:

Se , então:

Calculando os limites laterais:

Limite lateral pela esquerda:

Limite lateral pela direita:

Como os limites não laterais coincidiram, o limite não existe e, portanto, não é diferenciável em , como esperado! Em todos os outros pontos, a função será diferenciável.