A Equação de Diferenças Logística. Os problemas de 14 a 19 tratam da equação de diferenças (21) .
Seja o valor de para o qual a solução da Eq.(21) muda do período para o período . Então, como observado no texto, , e .
- Usando esses valores para , e , ou os que você encontrou no problema 18, calcule .
- Seja . Pode-se mostrar que tende a um limite quando , onde é conhecido como o número de Feigenbaum. Determine a diferença percentual entre o valor limite e , como calculado no item (a).
- Suponha que e use essa relação para estimar , o valor de para o qual aparecem soluções de período 16.
- Fazendo o gráfico ou calculando soluções próximas do valor de encontrado no item (c), tente detectar a aparição de uma solução de período 16.
- Observe que
.
Suponto que , e assim por diante, expresse como uma soma geométrica. Depois encontre o limite de quando . Isto é uma estimativa do valor de no qual começa a aparecer comportamento caótico na solução da equação logística (21).
Passo 1
Nesse exercício, vamos fazer os cálculos indicados em cada item com os valores dos itens exercícios anteriores. Faremos também gráficos com o auxilio de um software para plotar pontos.
Passo 2
- Vamos lá. Utilizando os valores que já nos é dado no enunciado (para facilitar nossas vidas), temos que:
- Bom, temos que a diferença percentual é definida como:
- Usando a mesma relação dada no item (a), porém agora para , teremos que:
- Nosso gráfico para esse valor de se torna algo do tipo:
- Esse item vai dar um pouquinho mais de trabalho, mas vamos lá! Pela forma que o enunciado nos da as igualdades, temos que
Passo 3
Substituindo e , teremos que
Passo 4
Isolando e substituindo nossos valores, teremos que:
Passo 5
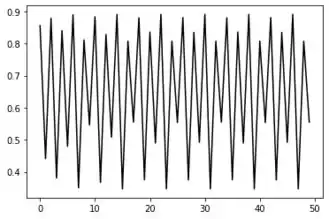
Onde temos uma solução de período 16 quando .
Passo 6
.
.
.
Se assumirmos que , vamos ter que:
Onde . Como queremos uma soma geométrica, temos que escrever na forma da mesma, assim:
E quando aplicamos limite a ela, chegamos em