Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 50

Esboce o gráfico da função

g (x) = ||x| - 1|

Passo 1

Fala aí, galerinha! 😉

Nesse problema temos apenas que esboçar o gráfico de g (x) = ||x| - 1| .

Parece complicado? 👀

Bom pessoal, neste exercício basta a gente olhar para a parte onde x é positivo e espelhar a função em relação a y .

Mas vamos resolver de um jeito mais técnico também.

Veja só! 😊

Passo 2

Primeiro, vamos “esquecer” do módulo que engloba a função toda.

Temos então que a primeira parte é h (x) = |x| - 1 . Vamos ver para quais valores esta equação pode ser negativa.

h (x) = |x| - 1 < 0 -> |x| < 1

Então:

( 1 ) {[[0 <= x <= 1 -> x],[- 1 < x < 0 -> - x]])

Agora vamos ver para quais valores esta equação vai ser positiva.

|x| - 1 > 0 -> |x| > 1

Então:

( 2 ) {[[x >= 1 -> x],[x <= - 1 -> - x]])

Tranquilo até aqui? 😉

Passo 3

Agora vamos a segunda parte, que considera o módulo que engloba a função.

Quando temos a parte (1), negativa, colocamos um sinal negativo no modulo:

g (x) = - ||x| - 1| = {[[s e 0 < x <= 1 -> g (x) = - x - (- 1) = - x + 1],[s e - 1 < x <= 0 -> g (x) = - (- x) + 1 = x + 1]])

Quando vale a parte (2), a gente despreza o módulo grande, pois a equação é sempre positiva.

g (x) = |x| - 1 {[[x - 1 s e x >= 1],[- x - 1 s e x <= - 1]])

Resumindo:

g (x) = {[[- x - 1 s e x <= - 1],[x + 1 s e - 1 <= x < 0],[- x + 1 s e 0 <= x < 1],[x - 1 s e x >= 1]])

Esboçando o gráfico, temos

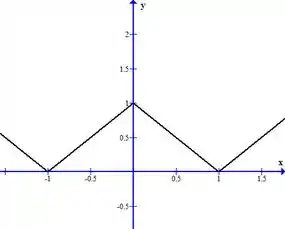
O que achou? Responde Aí! 😁

Resposta

g (x) = {[[- x - 1 s e x <= - 1],[x + 1 s e - 1 <= x < 0],[- x + 1 s e 0 <= x < 1],[x - 1 s e x >= 1]])

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine sef é par, ímpar ou nenhum dos dois. Se você tiver uma calculadora gráfica, use-a para verificar visualmente sua resposta. f x = x| x |
Esboce o gráfico:f (x) = |x| - 1
Esboce o gráfico:f (x) = |x| + |x - 2|
Esboce o gráfico:f (x) = |x + 1| - |x|
Esboce o gráfico:f (x) = ||x| - 1|