Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 25
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as curvas:
Temos uma função raiz e duas retas. Podemos calcular onde a reta intercepta o eixo e :
Agora a outra curva:
Agora esboçamos o gráfico:
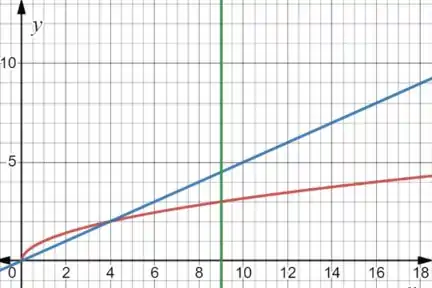
A curva vermelha é a reta azul é e a verde é .
Passo 2
A área que queremos esboçar é essa de verdinho:
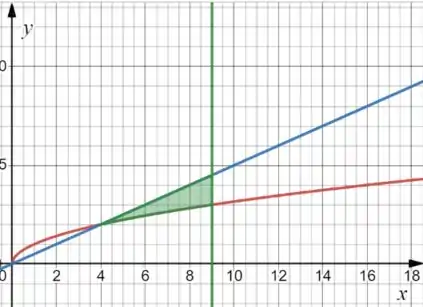
Então os limites de integração vão ser:
Para calcular o limite inferior a gente tem que calcular o ponto de intersecção entre as curvas:
Elevando os dois lados ao quadrado:
Passo 3
Organizando a integral, temos:
Resolvendo...
Então, isso resultará em:
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região entre a curva y = sec 2 x , - π 4 ≤ x ≤ π 4 , e o eixo x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região limitada pela parábola y = x - x 2 e pela reta y = - x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região no primeiro e quarto quadrantes, delimitadas pelas curvas y = 1 1 + x 2 e
16- Determine o centro de massa de uma placa fina que abrange a região limitada abaixo pela parábola y = x 2 e acima pela reta y = x , se a densidade da placa no ponto ( x , y ) for δ x = 12 x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada. A região limitada pelas parábolas y = 2 x 2 - 4 x e y = 2 x - x 2 .