Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 14

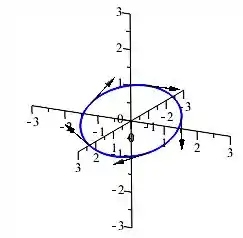
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.

r t = cos ⁡ t   i - cos ⁡ t j + sin ⁡ t k

Passo 1

Olá pessoal! Tranquilo?

Queremos esboçar o gráfico da seguinte função paramétrica, mostrando a direção em que o parâmetro cresce:

r t = cos ⁡ t i - cos ⁡ t j + s e n t k

Vamos começar entendendo o que fazer!

Precisamos construir o gráfico e para isso temos que identificar a curva, analisar as componentes de forma individual, substituindo valores de t e verificar a direção do parâmetro e por fim esboçarmos o gráfico.

Vamos começar?

Passo 2

As coordenadas x , y e z da equação paramétrica são respectivamente:

x = cos ⁡ t ,     ( 1 ) y = - cos ⁡ t ,     ( 2 ) z = s e n t ,     ( 3 )

Através de algumas substituições simples, utilizando ( 1 ) e ( 2 ) :

x = - y

E utilizando ( 1 ) e ( 3 ) :

x = cos ⁡ t ,     z = s e n ( t )

Substituindo na relação trigonométrica

x 2 + z 2 = cos 2 ⁡ ( t ) + s e n 2 t = 1

Assim, de acordo com as equações encontradas, concluímos que temos um círculo no eixo x z , cuja coordenada y vai aumentando conforme o valor de – x .

Logo, temos um círculo no problema, mas não é paralelo aos planos x y ou x z ou y z :

Passo 3

Para verificarmos de que forma o parâmetro t cresce, vamos observar alguns valores de t :

Para t = 0

x = cos ⁡ t = 1 ,     y = - cos ⁡ t = - 1 ,     z = s e n t = 0

Para t = π 2

x = cos ⁡ π 2 = 0 ,     y = - cos ⁡ π 2 = 0 ,     z = s e n π 2 = 1

Assim o parâmetro cresce seguindo o caminho:

1 , - 1,0 → ( 0,0 , 1 )

Passo 4

O gráfico da equação é:

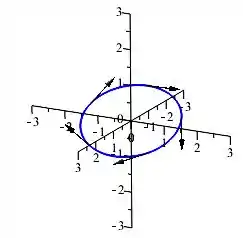
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a formula 11 para achar a curvatura.y = 4 x^(5 // 2)
Utilize o computador para traçar o gráfico da curva com equações paramétricas x = c o s , y = sen ⁡ 3 t , z = sen ⁡ t . Determine o comprimento total da curva com precisão de quatro casas decimais.
Use a regra de Simpson com n = 10 para estimar o comprimento do arco da cúbica retorcida x = t , y = t 2 , z = t 3 da origem até o ponto ( 2,4 , 8 ) .
Utilize uma calculadora gráfica ou um computador para traçar na mesma tela a curva e sua função curvatura k ( x ) . Esse é o gráfico que você esperava? y = x e - x
Determine o comprimento da curva dada.r (t) = t^2 i + 2 t j + ln t k , 1 = t = e