Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 13
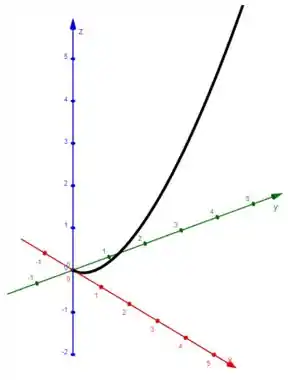
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.
Passo 1
E aii, tudo certo?
Queremos esboçar o gráfico da seguinte função vetorial, mostrando a direção em que o parâmetro cresce:
Como a gente não sabe a princípio o formato dessa curva, o que vamos fazer é ver como são as projeções nos planos , e (ou alguns desses planos).
Depois, o valor de para diferentes valores de vai nos indicar a direção que a curva é traçada quando o parâmetro cresce.
Passo 2
A função que estamos trabalhando é essa aqui:
A primeira coisa que a gente pode perceber é que esse gráfico vai estar só no primeiro octante (). Isso porque está elevado a uma potência par nas três coordenadas na função vetorial, então para qualquer valor de , as coordenadas , e serão positivas.
As equações paramétricas das coordenadas são:
Como e , vamos reescrever as coordenadas e em função de :
Tá, mas o que a gente faz com isso?
Bom, agora a gente pode esboçar as projeções da curva nos planos e .
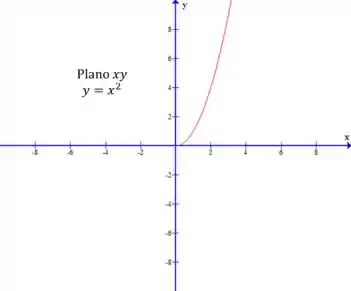
No plano , a projeção é parte de uma parábola:
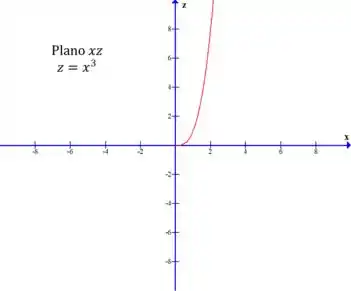
No plano , a projeção é parte de um gráfico de polinômio de 3º grau:
Então, o gráfico da curva fica assim:
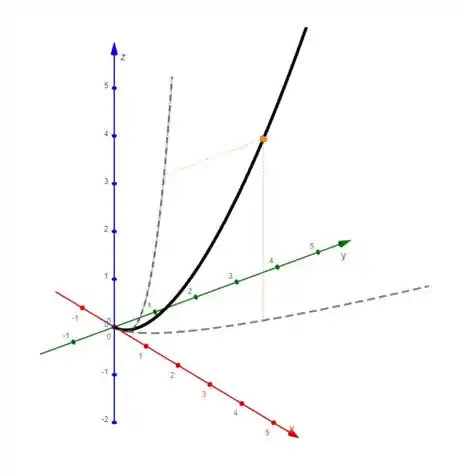
As curvas tracejadas são as projeções da curva nos planos e .
O ponto laranja mostra um exemplo de projeção da curva paramétrica nas curvas planas, que ajuda a gente a traçar o gráfico.
Resposta
