Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.2 - Ex. 31
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada.
Passo 1
Fala aí! tudo certinho?
Nesse problema queremos encontrar a integral de volume do solido gerado pelas curvas dadas em torno da reta .
Parece complicado?
Primeiro vamos esboçar a região sabendo que está limitada entre as curvas e .
Logo, a região que será rotacionada é:
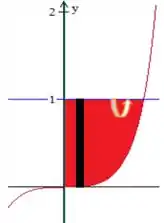
Ao rotacionarmos a figura em torno da reta , teremos um disco infinitesimal de raio:
Show?
Passo 2
A área do disco infinitesimal será:
O volume do sólido é dado pela expressão:
Vamos visualizar o sólido rotacionado:
E aí! o que achou? Responde Aí!
Resposta
Exercícios de Livros Relacionados
Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva x = y ² ² e x = y 4 , no primeiro quadrante
Ache o volume do solido gerado por rotação, em torno do eixo x da região limitada pela curva y = x c o s e c x , a reta x= 1 2 π , x= 1 4 π e eixo x.
Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva x = c o s y , a reta y = 1 6 π e eixo y
Ache o volume do sólido gerado pela rotação da região limitada pela curva y = sec 2 x , pelos eixo𝑠 e pelas reta x = 1 4 π em torno do eixo x .
Ache o volume do sólido gerado pela rotação da região limitada pela curva y = 3 csc 3 x pelo eixo x e pelas reta x = 1 6 π e x = 1 2 π em torno do eixo x .