Uma estrela variável é aquela cujo brilho alternadamente cresce e decresce. Para a estrela variável mais visível, Delta Cephei, o período de tempo entre os brilhos máximos é de dias, o brilho médio (ou magnitude) da estrela é , e seu brilho varia de em magnitude. Encontre uma função que modele o brilho de Delta Cephei como uma função do tempo.

E aí galera, beleza?

Essa questão é sobre modelagem de funções e transformação de gráficos! Ela é muito boa para a gente ter uma visão melhor de como na prática uma função modela um evento no nosso mundo, nesse caso, o brilho de uma estrela!

A primeira coisa que evemos atentar é que nos é dito que o evento ocorre em períodos de dias, ou seja, temos uma função periódica. Além disso, temos um valor máximo e mínimo para a nossa função ( acima de e abaixo), e assim nossa função periódica cresce e decresce alternadamente. Sabe o que isso lembra? Se você disse uma função seno, acertou! Se não disse, não esquenta que com esse passo a passo vais entender tudinho ;)

Dá uma olhada no jeitão do gráfico de uma função seno:

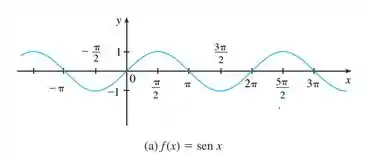
Esse aí é o gráfico de , que é a função seno mais simples que temos. Acontece que o nosso modelo não vai ser tão simples assim, ele será uma função seno deslocada e deformada.

Se a gente for escrever a forma completona da função seno que a gente vai usar, ela é desse jeito:

Onde o é o brilho da nossa estrela, o tempo em dias, o deslocamento na vertical do nosso gráfico, o fator de deformação na vertical, o fator de deformação na horizontal e o deslocamento na horizontal, beleza?

Veja só! 😬