Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.3 - Ex. 11

Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral.

A s   r e t a s   y = 2 x   ,   y = x 2   e   y = 3 - x

Passo 1

Faaaala, cara! Tranquileba?

Fazendo um esboço das funções, temos:

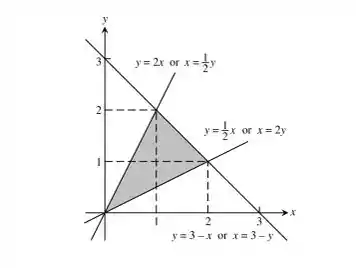
Nesse caso, temos que fazer a soma de integrais que correspondem a duas partes, ou seja, repare que temos que 0 ≤ x ≤ 1 e depois 1 ≤ x ≤ 2 na primeira, tendo que y em função de temos de x temos que é cortado pela reta y = x 2 assim, é deste ponto que ela se inicia, e s prossegue até 2 x , logo para a primeira parte, temos x 2 ≤ y ≤ 2 x , e para a segunda temos x 2 ≤ y ≤ 3 - x . Logo:

∫ 0 1 ∫ x 2 2 x d y   d x   +   ∫ 1 2 ∫ x 2 3 - x d y   d x

Passo 2

∫ 0 1 2 x - x 2 d x + ∫ 1 2 3 - x - x 2 d x

x 2 - 1 4 x 2 0 1 + 3 x - 1 2 x 2 - 1 4 x 2 1 2

1 - 1 4 + 6 - 2 - 1 - 3 - 1 2 - 1 4

3 4 + 3 - 9 4

3 2

Resposta

3 2

Exercícios de Livros Relacionados

Calcule a integral dupla. ∬ D y 2 d A D = x , y - 1 ≤ y ≤ 1 ,- y - 2 ≤ x ≤ y }
Determine o volume do sólido dado.Abaixo do plano z = 2 x + y 2 e acima da região limitada por x = y 2 e x = y 3 .
Calcule a integral dupla. ∬ D y 2 d A D é a região triangular com vértices 0,1 , 1,2 , 4,1 .
Uma carga elétrica é distribuída sobre o disco x 2 + y 2 ≤ 1 , de modo que a densidade de carga em x , y é σ x , y = x 2 + y 2 (medida em coulombs por metro quadrado). Determine a carga total no disco
Calcule a integral iterada. ∫ 0 1 ∫ 0 s 2 cos ⁡ s 3 d t d s