Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.1 - Ex. 3
Nos Exercícios 1-4, use aproximações finitas para estimar a área sob a curva da função, usando
a. uma soma inferior com dois retângulos de largura igual.
b. uma soma inferior com quatro retângulos de largura igual.
c. uma soma superior com dois retângulos de largura igual.
d. uma soma superior com quatro retângulos de largura igual.
3. entre e
Passo 1
O gráfico da função é:
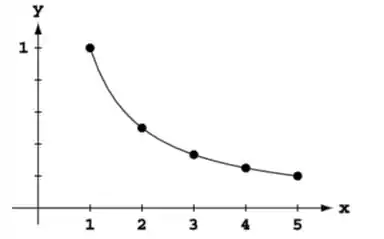
a.
Dois retângulos de base , como é uma soma inferior eles devem estar em baixo da curva, logo:
O primeiro terá uma altura igual a
E o segundo:
Agora fazendo o cálculo da área vamos obter:
Passo 2
b.
Quatro retângulos de base , como é uma soma inferior eles devem estar em baixo da curva, logo:
O primeiro terá uma altura igual a:
O segundo:
O terceiro:
O quarto:
Agora fazendo o cálculo da área vamos obter:
Passo 3
c.
Dois retângulos de base , como é uma soma superior eles devem estar em acima da curva, logo:
O primeiro terá uma altura igual a
E o segundo uma altura igual a
Agora fazendo o cálculo da área vamos obter:
Passo 4
d.
Quatro retângulos de base , como é uma soma superior eles devem estar em acima da curva, logo:
O primeiro terá uma altura igual a:
O segundo:
O terceiro:
E o quarto:
Agora fazendo o cálculo da área vamos obter:
Resposta
a.
b.
c.
d.