Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 17.2 - Ex. 11
Faça o gráfico da solução particular e de várias outras soluções. Que características essas soluções têm em comum?
Passo 1
Primeiramente nós solucionamos a equação característica da parte homogenia onde
que tem solução a solução da parte homogenia será:
Passo 2
Agora utilizaremos as técnicas dos coeficientes à determinar chutando uma solução particular do tipo
Suas derivadas ficam
e
onde
substituindo
Agrupando em
De fato, nós temos uma igualdade então os dois lados têm que ser iguais assim:
A solução da equação diferencial não homogenia será:
Passo 3
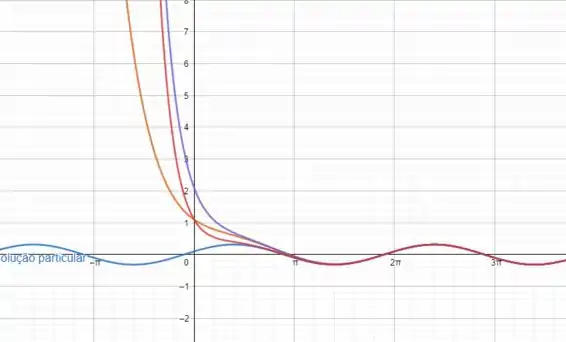
Notamos que quando tende para infinito as soluções convergem para a solução particular.
Resposta
Notamos que quando tende para infinito as soluções convergem para a solução particular.
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 a 6, use a fórmula de Euler para escrever a expressão dada na forma a + i b . exp 1 + 2 i
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. y ' ' + 6 y ' + 13 y = 0
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. 9 y ' ' + 9 y ' - 4 y = 0
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. y ' ' - 2 y ' + 6 y = 0
Em cada um dos problemas de 7 a 16, encontre a solução geral da equação diferencial dada. y ' ' - 2 y ' + 2 y = 0