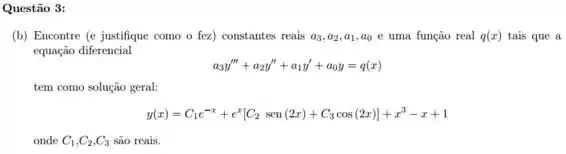Exercícios de Método dos Coeficientes Indeterminados - Lista de Exercícios Resolvida

Encontre a solução geral da equação diferencial abaixo:

Determine a solução geral da equação diferencial:

Com as seguintes condições iniciais

e .

Se , a equação diferencial tem uma solução da forma

(a)

(b)

(c)

(d) nenhuma das outras alternativas

(e)

1. Determine o conjunto dos valores de tais que a equação diferencial

Possui uma solução particular da forma

Se , a equação diferencial tem uma solução da forma

(a)

(b)

(c)

(d) nenhuma das outras alternativas

(e)

Determine a solução geral da equação diferencial linear de 2ª ordem não-homogênea com coeficientes constantes:

Determine a solução da equação diferencial linear de 2ª Ordem não-homogênea com coeficientes lineares, tomando ,

Considere a equação diferencial , onde e são constantes reais diferentes de zero. Então a solução geral da equação diferencial é (onde e são constantes reais arbitrárias):

Resolva os problemas de valor inicial abaixo, isto é, encontre a função que satisfaz a equação diferencial e as condições iniciais dadas.

(c)

Considere a EDO:

Note que é uma solução da equação homogênea associada...

(a) Encontre a solução geral da equação homogênea associada a

(b) Determine a solução geral de (2).

(c) Determine a solução do PVI dado por (2), e .

(d) Faça o gráfico desta solução no Mathematica. Para quais valores de , aproximadamente, temos positivo?

Considere a série de funções trigonométricas

1. Analise a convergência pontual e uniforme da mesma;
2. Denotando a soma da série por , prove que é contínua em [0,1];
3. Determine o valor dos coeficientes na identidade , justificando os cálculos.

Resolva o PVI

Encontre todas as soluções da EDO:

Encontre todas as soluções da EDO:

Considere a equação

Onde b e c

1. Determine de forma que seja a solução da EDO acima.
2. Utilizando os valores de e encontrados no item anterior, determine a solução geral de

Usando o método de coeficientes indeterminados, encontre a solução geral da equação diferencial

Considere a EDO não-homogênea , onde

1. Encontre a solução geral da EDO homogênea associada;
2. Encontre uma solução particular da EDO não-homogênea; e
3. Dê a solução geral da EDO.

Determine a solução geral da equação diferencial:

Uma solução particular de

É do tipo:

Uma função se diz limitada se existem uma constante tal que para todo o . Qual o valor de tal que a equação diferencial

Não tenha soluções limitadas?

Determine a solução geral da equação diferencial linear de ordem não-homogênea com coeficientes constantes:

Onde , . Tome . Considere .

Teste 7: Considere os problemas

e

Analise as seguintes afirmações:

1. A solução do segundo problema possui um ponto de inflexão na origem.
2. A equação linear possui pelo menos uma solução par.
3. Todas as soluções da equação linear são ímpares.

São verdadeiras:

1. Apenas .
2. Apenas e .
3. Apenas e .
4. Apenas e .
5. Apenas .

Questão 4: Qual é a solução da equação diferencial satisfazendo a condição inicial ?

2. .
3. .
4. .
5. Nenhuma das demais alternativas.

Teste 8: Um menino utiliza um estilingue para disparar verticalmente para cima uma pedra de massa a uma velocidade inicial . A resistência do ar exerce um amortecimento do movimento proporcional à velocidade do corpo, exercendo uma força de intensidade quando a velocidade da pedra é , sendo consatante. Considerando que a aceleração da gravidade é constante e igual a , então a altura máxima atingida pela pedra é:

Questão 3: Sejam e duas soluções da equação diferencial

Suponha que . Então podemos afirmar que, para todo , temos:

1. , para algum .
2. , para algum .
3. , para algum .
4. , para algum .
5. , para algum .

Calcule a solução geral da EDO .

Um sistema massa-mola é governado pelo problema de valores iniciais:

A posição da mola no instante é:

Determine a solução geral da equação diferencial linear de 2ª ordem não homogênea com coeficientes constantes:

Questão 1 - Determine a solução geral da seguinte EDO.

Questão 3 - Determine uma solução particular da EDO .

Determine a solução geral da equação diferencial linear de ordem não-homogênea com coeficientes constantes:

Sabendo que .

Pela segunda lei de Newton, um objeto de massa em queda livre, com atrito de viscosidade com o ar , obedece a equação diferencial:

onde é a posição vertical em metros e usamos a aproximação da constante gravitacional da Terra .

Dado que , ,temos que é:

[Na resposta e^{-k} significa ]

Escolha uma:

Sabendo-se que tem uma solução particular da forma , para alguma constante real . Então, quanto vale ?

Resolva as equações diferenciais lineares não homogêneas com coeficientes constantes:

b)

Sabendo que , é solução geral de uma equação homogênea da forma , com b, c constantes, determine b e c e encontre a solução geral da equação não-homogênea

Calcule a solução geral da EDO.

Considere:

em que é uma constante. Seja a solução dada por uma série de potências

1. Encontre uma regra para determinar os coeficientes

2. Encontre o coeficiente .

3. Considere agora

Em que é um número par positivo. Encontre uma solução que seja um polinômios de grau .

Questão 3 (Justifique todas as suas respostas):

Encontre a solução do PVI:

Se e são duas soluções particulares da equação não homogênea , a diferença é:

(a) A solução geral da mesma equação

(b) Uma solução particular da equação homogênea

(c) A solução geral da mesma equação homogênea

(d) Uma solução particular da mesma equação

(e) Nenhuma das outras opções.

Usando o método dos coeficientes indeterminados, determine a solução geral das EDO’s:

a)

Usando o método dos coeficientes indeterminados, determine a solução geral das EDO’s:

b)

Questão 4: (Justifique todas as suas respostas)

Encontre a solução do seguinte PVI:

Encontre a solução geral da equação diferencial

a) Determine a solução geral da equação diferencial:

b) Determine o valor de de modo que a solução da equação acima com condições iniciais e seja limitada no intervalo .

A equação diferencial tem uma solução da forma, com , :

nenhuma das demais

A solução geral de pode ser escrita na forma , onde é a solução da equação homogênena associada e É da forma:

Lembre que . A equação tem uma solução particular da forma (onde as letras minúsculas representam constantes arbitrárias):

1. .
5. Nenhuma das demais alternativas.

Determine uma equação diferencial de modo que a função

seja a solução geral da EDO.

1. Considere a EDO

onde .

Suponha que a equação característica da EDO acima possui duas raízes distintas sendo uma delas, mostre que podemos encontrar uma solução particular na forma , onde

Explique como sabemos que .

Sabe-se que tem uma solução particular da forma , para alguma constante real . Então:

5. Nenhuma das demais alternativas.

Determine a solução geral das equações diferenciais não homogênea

Determine a solução geral das equações diferenciais não homogênea

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Determine a solução geral das equações diferenciais não homogênea

Determine a solução geral das equações diferenciais não homogênea

Resolva os seguintes

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Resolva os seguintes

Resolva as EDO´s não homogêneas

Resolva as EDO´s não homogêneas

Resolva os seguintes