Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.5 - Ex. 41
Formas extravagantes podem ser criadas usando-se a capacidade de traçar funções definidas implicitamente de um SCA.
- Faça o gráfico da curva com equação
- Encontre as equações das retas tangentes nos pontos e .
- Encontre as coordenadas exatas nos pontos da parte (a).
- Crie curvas mais extravagantes ainda modificando a equação da parte (a).
Em quantos pontos essa curva tem tangentes horizontais?
Passo 1
Nessa questão queremos encontrar o gráfico de uma curva dada por:
Usando um SCA (Sistema de computação algébrica). Depois de feito o gráfico, vamos analisar onde o gráfico possui retas tangentes horizontais, as retas tangentes em dois pontos e por fim vamos brincar de fazer curvas no SCA mexendo na equação dada.
Aqui vamos lembrar que a equação da reta tangente em um ponto é dada por:
Onde é a inclinação da reta que pode ser calculada fazendo a derivada da função no ponto.
E para derivar essa função implicitamente devemos derivar de ambos os lados da expressão, e sempre que derivarmos em devemos multiplicar por .
Passo 2
- O gráfico da curva é o seguinte:
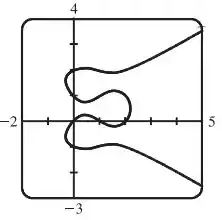
Olhando o gráfico vemos que há oito pontos com tangentes horizontais, localizados aproximadamente em e .
Passo 3
A gente acha as equações da reta tangente derivando nossa curva, então:
Só lembrando que a curva é dada por:
Antes de derivar, vamos realizar essas multiplicações, pois parece que ficará mais fácil.
Derivando implicitamente temos:
Organizando:
E deixando em evidência.
E substituindo o ponto , obtemos:
De forma que a reta tangente será:
Já no ponto iremos obter:
E substituindo na reta tangente, obtemos:
Passo 4
Para encontrar analiticamente os pontos onde a reta tangente é horizontal, basta fazer que a derivada vale zero.
O que só é verdade se
Resolvendo essa equação de segundo grau, obtemos os seguintes valores de .
Passo 5
Multiplicando o lado direito da equação por , a gente obtém o primeiro gráfico.
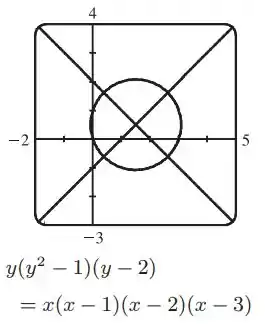
Modificando a equação de outras maneiras, podemos gerar os gráficos a seguir:
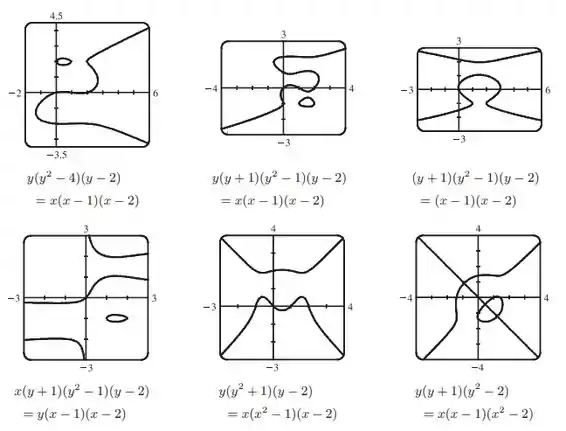
Resposta
Questão téorica, resposta nos passos.