Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 80
- Mostre que para .
- Deduza que
Passo 1
E aí, pessoal!
Nesse problema temos que mostrar que em e também temos que mostrar que
Tem ideia de como fazemos isso?
Então para o item (a) temos que analisar a função e seu intervalo, e determinar qual é maior que a outra.
Para o item (b) vamos usar uma propriedade, aquela de que se uma função é maior que a outra, a integral também será maior para o mesmo intervalo, então:
Se
Então
E também precisamos ter em mente essa primitiva antes de sair integrando é:
Agora sim bora resolver!
Passo 2
Para o intervalo nós temos que
Como a fórmula do cosseno é
e a hipotenusa é maior que o cateto, elevando essa fórmula ao quadrado temos um número cada vez menor, então:
Como é uma função decrescente em , .
Para ficar mais claro ainda, vamos ser no gráfico:
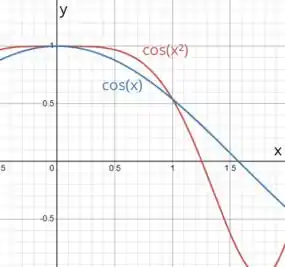
Show?
Passo 3
Para o item b), temos que
então, usando nossa demonstração da parte (a), temos que em .
Portanto:
Agora vamos resolver apenas a integral do lado direito:
Analisando os limites de integração:
Agora que resolvemos essa, vamos substituir a integral pelo seu valor na nossa desigualdade, e temos em fim:
E aí! entendeu tudo? Responde Aí!
