(a) A função
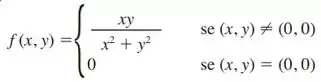
corresponde ao gráfico da Figura 4. Mostre que e existem, mas não é diferenciável em . [Sugestão: Utilize o resultado do Exercício 45.]
(b) Explique por que e não são contínuas em .
Passo 1
Oie, vamos resolver essa atividade juntos agora.
A gente tem a função a seguir:
Devemos mostrar que e no ponto existem, mas que a nossa função não é diferenciavel neste ponto.
Para isso nós iremos utilizar as definições de derivadas, com limites, para provarmos cada uma dessas proposições:
E
Nos atentando para o fato de que temos uma função dada por condicional.
Para a letra , sabemos que uma função deve ser continua se e , então deveremos mostrar que ou os limites não existem ou eles são diferentes dos valores dessas funções.
Passo 2
(a) Para calcular as derivadas desta função, vamos ter que usar a definição, então
Substituindo os valores:
Podemos dize que
Temos então que:
Repetindo o processo para :
Podemos dize que
Teremos então:
As derivadas parciais de em existem e são .
Passo 3
Se olharmos agora para o limite da função, quando
Vamos agora calcular o limite, a gente pode tomar diferentes caminhos para chegar em . Se pegarmos o caminho :
Como :
Temos então:
Se nos aproximarmos por :
Como :
Simplificando:
Teremos então:
Como a função se aproxima com dois valores diferentes, o limite não existe.
No exercício 45 achamos que se uma função é diferenciável, então ela é contínua, se não é contínua, então ela não é diferenciável, apesar de suas derivadas parciais existirem em todo o domínio.
Passo 4
(b) Podemos calcular e para valores diferentes de , como sendo
Para ser continua em temos que provar que o limite seja , como calculamos em (a)
Usando o caminho :
Nos sobre apenas :
Vamos simplificar:
Temos então esse resultado:
Como o limite não existe, a função derivada é descontínua.
Podemos de maneira similar fazer com
Calculando o limite
Usando o caminho
Temos então só :
Teremos então o resultado:
O limite não existe e a função derivada é descontínua.
Resposta
Ver o desenvolvimento