Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 36
Hipocicloide - Quando um círculo rola dentro de um círculo fixo, qualquer ponto P na circunferência do círculo que rola descreve uma hipocicloide. Seja o círculo fixo, seja b o raio do círculo que rola, e seja a posição inicial do ponto P traçado. Encontre equações paramétricas para a hipocicloide, utilizando como parâmetro o ângulo u a partir do eixo x positivo até a reta que une os centros dos círculos. Em particular, se , assim como na figura a seguir, mostre que a hipocicloide é a astroide
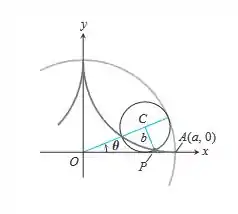
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A equação que descreve a posição do ponto P no eixo
Nós podemos simplificar da seguinte forma
Depois de substituir por , este é o resultado, mas ainda precisa de alguns ajustes.
Vamos pensar na situação, como , podemos fazer a seguinte manipulação
Passo 2
Agora, vamos trabalhar na simplificação da expressão acima, podemos considerar que , com isso, temos que
Manipulando um pouco mais,
podemos obter isso após alguns cálculos com a etapa anterior
Passo 3
Se baseando na geometria da figura dada no enunciado, obtemos que
E com isso,
O mesmo que ao provar a equação paramétrica para x.
E com isso, é igual a
De forma análoga,