Um homem com 6 de altura está caminhando a uma taxa de por segundo em direção a um poste de iluminação, com de altura (ver figura a seguir).
(a) A que taxa está variando o comprimento da sombra?
(b) Com que rapidez está se movendo a extremidade de sua sombra?
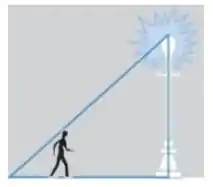
Passo 1
Pra começar vamos chamar a distância do homem até o poste, em um instante qualquer de , e o tamanho da sombra do homem de
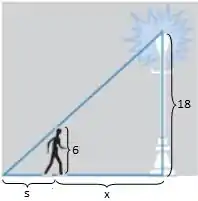
Agora vamos usar uma pitadinha de geometria hehe. Tá vendo que o triângulo formado pelo homem e pela sombra é igualzinho o triângulo formado pelo poste e pelo chão? Obviamente numa versão menor. Então, podemos falar que esses dois triângulos são semelhantes, então a razão entre os comprimentos dos seus lados é igual:
PS: poderíamos chegar nessa mesma conclusão olhando pra tangente do ângulo comum aos dois triângulos.
Mexendo um pouco nessa expressão:
Passo 2
Pra relacionar as taxas podemos derivar essa expressão em relação ao tempo:
Passo 3
(a)
Já que queremos saber a que taxa está variando o comprimento da sombra, estamos interessados no .
Mas o enunciado nos diz que o homem está caminhando a uma taxa de por segundo, isso nos diz que:
Lembrando que como ele está se aproximando do poste, está DIMINUINDO e por isso o sinal de menos.
Se substituirmos esses dados na equação (1):
Repare que encontramos o que faz bastante sentido já que o comprimento da sombra está aumentando 😊
Passo 4
(b)
Pra essa vamos ter que pensar um pouco no que está acontecendo.
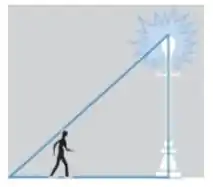
Você concorda que o comprimento da sombra aumenta porque as duas extremidades dela estão se movendo? Uma extremidade fica no pé do homem e se move com a velocidade dele, e a outra fica naquela quina ali (e é nessa que estamos interessados).
Pensando nisso podemos falar que a velocidade com que a sombra aumenta nada mais é com que a soma das velocidades de suas extremidades, só que uma das extremidades tá ali no pé do homem e anda com a mesma velocidade dele:
Resposta
(a)
(b)