Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 22

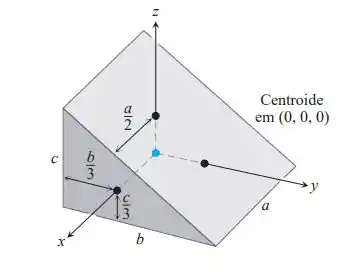
Momentos de inércia: os eixos coordenados na figura passam pelo centroide de uma cunha sólida paralelos às arestas identificadas. Encontre I x ,   I y ,   I z se a = b = 6   e c = 4 .

Passo 1

Faaaala, cara! Tranquileba?

A projeção da base da cunha no plano Oxy corresponde ao retângulo de lados:

- a 2 < x < a 2   e   - b 3 < y < 2 b 3

Além disso, calculando, obtém-se que a face superior da cunha está contida no plano de equação z = - c y b + c 3 . Segue-se que a cunha pode ser descrita como:

- a 2 < x < a 2 ,           - b 3 < y < 2 b 3     e     - c 3 < z < - c y b + c 3  

Passo 2

Assim, para I x :

I x = ∫ - 3 3 ∫ - 2 4 ∫ - 4 3 - 2 3 y + 4 3 y 2 + z 2   d z   d y   d x

∫ - 3 3 ∫ - 2 4 y 2 z - 4 3 1 3 4 - 2 y + 1 3 z 3 - 4 3 1 3 4 - 2 y d y   d x

∫ - 3 3 ∫ - 2 4 ( 8 y 2 3 - 2 y 3 3 + 8 2 - y 3 81 + 64 81 )   d y   d x

(essa parte é uma conta bem extensa então vou economizar espaço, amigo, mas escolhas difíceis requerem determinação forte hahaha se quiser encontrar o valor, sinta-se livre)

∫ - 3 3 104 3   d x  

104 3 x - 3 3

I x = 208 .

Para I y :

I y = ∫ - 3 3 ∫ - 2 4 ∫ - 4 3 1 3 4 - 2 y y 2 + z 2   d z   d y   d x

∫ - 3 3 ∫ - 2 4 x 2 z - 4 3 1 3 4 - 2 y + 1 3 z 3 - 4 3 1 3 4 - 2 y d y   d x

∫ - 3 3 ∫ - 2 2 4 - 2 y 3 81 + x 2 4 - 2 y 3 + 4 x 2 3 + 64 81   d y   d x

∫ - 3 3 12 x 2 + 32 3 d x

4 x 3 - 3 3 + 32 3 x - 3 3

I y = 280

Passo 3

E finalmente, para I z :

I z = ∫ - 3 3 ∫ - 2 4 ∫ - 4 3 1 3 4 - 2 y x 2 + y 2   d z   d y   d x  

∫ - 3 3 ∫ 2 4 ( x 2 + y 2 z - 4 3 1 3 4 - 2 y )   d y   d x

∫ - 3 3 ∫ - 2 4 x 2 + y 2 1 3 8 - 2 y d y   d x

12 ∫ - 3 3 x 2 + 2   d x

12 1 3 x 3 - 3 3 + 2 x - 3 3

I z = 360  

Resposta

I x = 208 .

I y = 280

I z = 360  

Exercícios de Livros Relacionados

Calcular o momento de inércia do hemisfério x 2 + y 2 + z 2 ≤ 1 ,x ≥ 0 em relação ao eixo y . A densidade no ponto P ( x , y , z ) é proporcional à distância de P ao plano y z .
Calcular o momento de inércia em relação ao eixo dos x do sólido delimitado por z = x 2 + y 2 e z = 4 . A densidade de massa em um ponto P x , y , z é dada por x 2k g / m 3 .
Calcular o momento de inércia em relação aos eixos coordenados do sólido delimitado por z = 4 - x 2 - y 2 e z = 0 , sabendo que a densidade de massa em um ponto P é proporcional à distância de P ao pl
(Teorema de Steiner ou dos iexos paralelos). Seja I c m o momento de inércia em relação a um eixo que passa pelo centro de massa de um corpo e I o momento de inércia em relação a um eixo paralelo, a u
Calcule o momento de inércia de um sólido homogêneo com a forma de um cone circular reto de altura h e o raio da base R , em relação a um eixo passando pelo vértice e perpendicular ao eixo do cone.