Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.1 - Ex. 68

Em quais números a seguinte função g é derivável?

g x = - 1 - 2 x   ,   s e   x < - 1 x 2   ,   s e - 1 ≤ x ≤ 1 x     ,     s e     x > 1

Dê uma fórmula para g ' e esboce os gráficos de g e g '

Passo 1

Fala aí! Tudo certinho?

Nessa questão foi dada a função:

g x = - 1 - 2 x   ,   s e   x < - 1 x 2   ,   s e - 1 ≤ x ≤ 1 x     ,     s e     x > 1

Queremos saber se g é derivável.

Para saber se ela é derivável em todos os pontos podemos estudar onde poderíamos tem problemas de comportamento ou de domínio na função.

Veja que para valores de x < - 1 , a função assume a forma:

g x = - 1 - 2 x

Essa é uma função polinomial, e toda função desse tipo é derivável em todo o seu domínio.

Já para - 1 ≤ x ≤ 1

g x = x 2

Que também é derivável para todos os valores de x .

E para x > 1

g x = x

Que também é derivável.

Ou seja, cada intervalo é formado por funções bem comportadas. O grande problema é justamente nos extremos dos intervalos, pois ali não sabemos se existe algum salto da função ou uma mudança abrupita de comportamento.

Por isso vamos analisar esses pontos específicos aplicando a derivada, expressa pela sua definição, pela esquerda e direita de 1 e de - 1 .

Ou seja, faremos:

    g + ' ( 1 )           e           g - ' ( 1 )    

E também

    g + ' ( - 1 )           e           g - ' ( - 1 )    

Caso os pares sejam iguais, a funçaõ g ( x ) será derivável no ponto estudado.

Veja só!

Passo 2

Pela definição, temos:

g + ' 1 = lim h → 0 + ⁡ g 1 + h - g 1 h

g + ' 1 = lim h → 0 + ⁡ 1 + h - 1 h

g + ' 1 = lim h → 0 + ⁡ 1 = 1

E

g - ' 1 = lim h → 0 - ⁡ g 1 + h - g 1 h

g - ' 1 lim h → 0 - ⁡ 1 + h 2 - 1 2 h

g - ' 1 = lim h → 0 - ⁡ h 2 + 2 h h

g - ' 1 = lim h → 0 - ⁡ ( h + 2 ) = 2

Veja que g + ' ( 1 ) ≠ g - ' ( 1 ) , portanto g não é derivável em 1.

Passo 3

Vamos ver agora para - 1 :

g + ' - 1 = lim h → 0 + ⁡ g - 1 + h - g - 1 h

  g + ' - 1 = lim h → 0 + ⁡ - 1 + h 2 - - 1 2 h

g + ' - 1 = lim h → 0 + ⁡ h 2 - 2 h h

g + ' - 1 = lim h → 0 + ⁡ h - 2

g + ' - 1 = - 2

e

g - ' - 1 = lim h → 0 - ⁡ g - 1 + h - g - 1 h

g - ' - 1 = lim h → 0 - ⁡ - 1 - 2 - 1 + h - - 1 - 2 - 1 h

g - ' - 1 = lim h → 0 - ⁡ - 2 h h

g - ' - 1 = lim h → 0 - ⁡ - 2

g - ' - 1 = - 2

Veja que g + ' - 1 = g - ' - 1 , portanto g é derivável em - 1 .

A função g é contínua para cada intervalo, logo podemos dizer que g é derivável para qualquer x , exceto x = 1 .

Show?

Passo 4

Derivando cada intervalo, temos: g ' x = - 2   ,   s e   x < - 1 2 x   ,   s e - 1 ≤ x < 1 1   ,   s e     x > 1

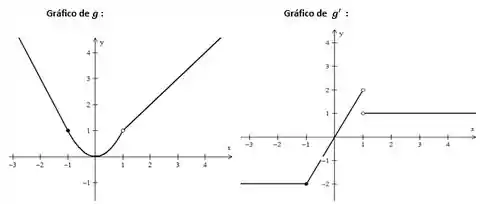
Veja como nossa resposta faz sentido olhando para o gráfico. O gráfico da derivada dá um salto justamente em x = 1 .

E olhando para o gráfico da função, vemos que ela tem uma mudança de comportamento justamente nesse ponto.

E aí! Entedeu tudo? Responde Aí!

Resposta

f não é derivável em 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d
Nos exercicos de 1 a 20, faça o seguinte: (a) Trace um esboço gráfico da função; (b) determine se f é continua em x 1 ; (c) calcule f ’ - ( x 1 ) e f ’ + ( x 1 ) , se existirem; (d) determine se f é d