Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 18
Uma partícula começa na origem, se move ao longo do eixo para o ponto , em seguida ao longo do quarto da circunferência para o ponto , e então para baixo pelo eixo até a origem. Use o Teorema de Green para encontrar o trabalho feito nessa partícula pelo campo vetorial
Passo 1
Faala, pessoal!
Nessa questão, temos que encontrar o trabalho realizado por um campo vetorial em uma partícula ao longo de um caminho . Isso é calculado assim:
Pra resolver isso, vamos usar o Teorema de Green, que diz que se é uma curva fechada e a região dentro dessa curva, então:
Vamos começar olhando pra trajetória dessa partícula pra definir quem é e quem é . Daí, definimos os limites de integração de , pra podermos aplicar o teorema.
Nesse caso, como estamos em uma região circular, vamos usar coordenadas polares:
Sem esquecer do jacobiano, que nesse caso é
Definidos os limites de integração, vamos calcular o termo , pra montarmos a integral dupla e calcular!
Passo 2
A trajetória da partícula é:
“começa na origem, se move ao longo do eixo para o ponto , em seguida ao longo do quarto da circunferência para o ponto , e então para baixo pelo eixo até a origem”
Colocando isso num desenho fica assim:
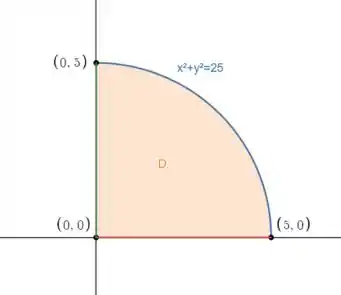
Então ela começa na origem, anda primeiro na reta vermelha, depois pelo arco em azul e por último na reta verde.
A região que se forma é um quarto de círculo.
Para usarmos coordenadas polares, fica assim:
Como estamos no primeiro quadrante,
E como o círculo tem raio ,
Ah, nunca esquece do jacobiano!!
Então a integral fica:
Passo 3
Agora a gente tem que descobrir quem é esse .
O campo vetorial é
Então
Primeiro, derivamos em função de , com constante:
E derivando em função de , com constante:
E a integral fica:
Mas em coordenadas polares, , então:
Passo 4
Falta só resolvermos essa integral, de dentro pra fora:
Primeiro integramos em função de , com constante:
E por último, integramos em função de :
E achamos o valor do trabalho: