Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 17
Calcule a integral tripla
Onde é limitado pelo parabolóide e pelo plano
Passo 1
Opa, tudo certinho? Temos uma questão que nos pede o cálculo do volume de uma região entre um parabolóide qualquer e um plano . Temos que encontrar uma forma de representar os limites desses paraboloide e desse plano nos limites de integração. Veja que em muitos casps vale a pena transformar a equação do parabolóide em coordendas cilíndricas, e esse é um desses casos, pois facilita e muito a solução do exercício.
Nessa questão aqui, o parabolóide não tá escrito de forma usual. Geralmente a gente tem a equação do tipo , só que agora a nossa equação é . Desse jeito não vai ser tão diferente do que a gente tá acostumado, mas tem que prestar atenção pra não dar mole, beleza?
Como o nosso parabolóide é paralelo ao eixo vamos usar o sistema de coordenadas cilindricas definido da seguinte forma
Show ? É como se tivessemos feito uma rotação de eixos!
E o jacobiano é aquele mesmo de coordenadas cilindricas, então
Beleza! A nossa integral então vai ficar
Passo 2
Agora temos que determinar os limites de integração! Só pra guiar a gente, aqui um esboço do parabolóide e do plano
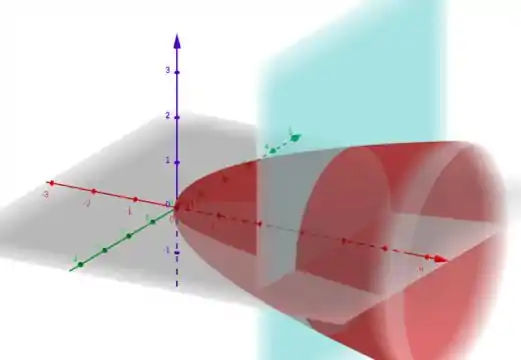
Veja que o eixo em azul é o eixo , em vermelhor o eixo e em verde o .
Vamos escrever a integral em função de , sabemos que é limitado em , pelo plano. Então já temos que
Mas como
Então vamos ter
Perceba que a figura faz uma voltla completa em relação ao eixo . De modo que:
Show! Agora é só montar a integral!
Passo 3
A nossa integral fica assim
Então
Substituindo os valores de e .
Temos:
Resolvendo a potência:
Substituindo:
Resolvendo a integral:
Finalizando temos:
Show! O resultado da nossa integral será
Show! Conseguimos :D