Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 77
77. Se para em e para e , em que pontos você conhece automaticamente que ? O que se pode dizer sobre o valor do limite nesses pontos?
Passo 1
Vamos olhar para os gráficos das funções e :
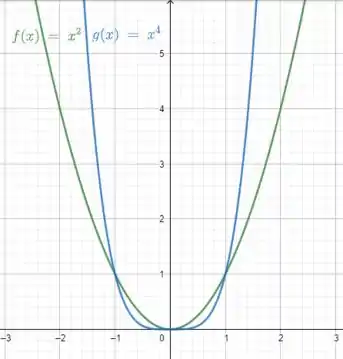
Nós sabemos que está entre os dois gráficos:
Abaixo de e acima de entre e
E abaixo de e acima de para valores menores que e maiores que
Portanto, só iremos conseguimos saber algo do limite de quando estiver tendendo a . Pois nesses pontos vai valer o mesmo valor que e .
Passo 2
Podemos mostrar isso algebricamente:
só ira ser conhecido quando
Pois quando isso acontece , então
Então
logo
Ou
Passo 3
O valor do limite nesses pontos vai ser de
e
e
Resposta
Exercícios de Livros Relacionados
Mostre que: 1 1 ⋅ 3 + 1 3 ⋅ 5 + … + 1 2 n - 1 2 n + 1 = n 2 n + 1 Sugestão: 1 2 n - 1 2 n + 1 = 1 2 1 2 n - 1 - 1 2 n + 1 .Use o resultado de (a) para calcular: lim n → ∞ ∑ k = 1 n 1 2 k - 1 2 k + 1
Os gráficos de f e g são dados. Use-os para calcular cada limite. Caso não exista, explique o por quê. lim x → 2 f x + g x lim x → 1 f x + g x lim x → 0 f x g x lim x → - 1 f x g x lim x → 2
Tomando por base o Exemplo 6, poderíamos conjecturar que a aproximação pelo ponto médio sempre fornece uma aproximação melhor do que as aproximações pelas extremidades. Discuta os méritos dessa conjec
Escrevendo por extenso as somas, determine se são válidas as seguintes identidades: ∫ ∑ i = 1 n f i x = ∑ i = 1 n ∫ f i x d d x ∑ i = 1 n f 1 x =∑ i = 1 n d d x f i x
Prove a parte ( c ) do Teorema 5.4 . 1 .