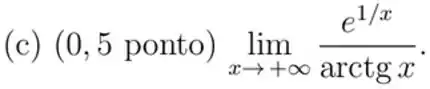Exercícios de Introdução aos Limites e suas Propriedades - Lista de Exercícios Resolvida
Questão 1
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Obs: considere
Ver solução completaQuestão 9
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 11
Cada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
b.
Ver solução completaQuestão 13
Cada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
a.
Ver solução completaQuestão 14
Cada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
c.
Ver solução completaQuestão 15
Cada um dos exercícios a) - d) dá uma função , um ponto e um número positivo . Determine . Em seguida, determine um número δ > 0 de modo que para todo x
d.
Ver solução completaQuestão 19
Considere a seguinte proposição: Se , então
- e é um exemplo para a proposição?
- A proposição é verdadeira ou falsa?
Questão 20
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 22
Calcule ou argumente que os valores não existem. Em todos os casos justifique seus cálculos e respostas.
Ver solução completaQuestão 24
Considere a função , dada por:
b) O que podemos afirmar sobre . Justifique sua resposta.
Ver solução completaQuestão 25
Considere a função dada por
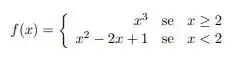
b) Calcule os seguintes limites, justificando suas respostas:
Ver solução completa
Questão 26
Esboce gráficos e use argumentos de aproximação para calcular os seguintes limites:
b)
Ver solução completaQuestão 28
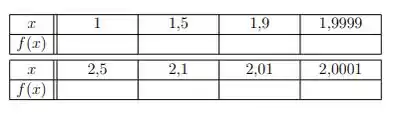
Estime algebricamente o valor do limite usando os valores de fornecidos. Use uma calculadora.
Questão 31
Considere a função
(a) Faça o gráfico de
(b) Utilize o gráfico do item (a) para determinar
(c) Utilize o gráfico do item (a) para determinar
(d) Utilize o gráfico do item (a) para determinar
(e) Utilize o gráfico do item (a) para determinar
(f) Utilize o gráfico do item (a) para determinar
Ver solução completaQuestão 32
Considere a função f cujo gráfico está representado abaixo. Determine o que se pede.
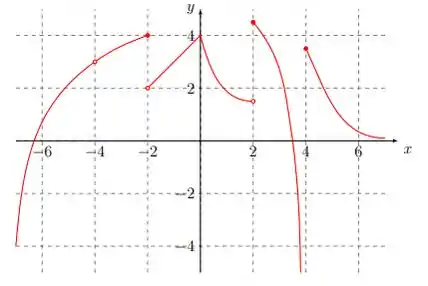
(a) O domínio de .
(b) e o limite
(c) e o limite
(d) e o limite
(e) e o limite
(f ) e o limite
(g) O que se pode dizer sobre a existência do limite nos pontos ?
Ver solução completaQuestão 34
1) Se a posição de um carro no instante é dada por , então a velocidade média entre os instantes e é dada por
Quanto mais próximo estiver de zero, mais perto a velocidade média estará da velocidade em , de modo que essa velocidade vale
Para cada função abaixo, simplifique o quociente que dá a velocidade média entre os intentes e . Em seguida, calcule a velocidade fazendo se aproximar de zero.
(a) , no ponto
(b) , no ponto
(c) , no ponto
(d) , com , , em um ponto genérico.
Dica: para o item (b), lembre que ; para o item (c), multiplique o numerador e o denominador por
Ver solução completaQuestão 35
Questão 1. Avalie os limites abaixo e encontre o correspondente valor caso exista. justifique suas respostas.
d)
Ver solução completaQuestão 38
Considere funções com limitada. Assinale a afirmação incorreta
- Se , para todo e , então
- Se , então
- Se , então
- Se , então
- Se , então
Questão 39
Considere funções com limitada. Assinale a afirmação incorreta
- Se , para todo e , então
- Se , então
- Se , então
- Se , então
- Se , então
Questão 45
Encontre o valor de para que o seguinte limite exista e calcule o seu valor:
Ver solução completaQuestão 46
1) Se a posição de um carro no instante é dada por , então a velocidade média entre os instantes e é dada por
Quanto mais próximo estiver de zero, mais perto a velocidade média estará da velocidade em , de modo que essa velocidade vale
Para cada função abaixo, simplifique o quociente que dá a velocidade média entre os intentes e . Em seguida, calcule a velocidade fazendo se aproximar de zero.
(a) , no ponto
(b) , no ponto
(c) , no ponto
(d) , com , , em um ponto genérico.
Dica: para o item (b), lembre que ; para o item (c), multiplique o numerador e o denominador por
Ver solução completaQuestão 47
1) Se a posição de um carro no instante é dada por , então a velocidade média entre os instantes e é dada por
Quanto mais próximo estiver de zero, mais perto a velocidade média estará da velocidade em , de modo que essa velocidade vale
Para cada função abaixo, simplifique o quociente que dá a velocidade média entre os intentes e . Em seguida, calcule a velocidade fazendo se aproximar de zero.
(a) , no ponto
(b) , no ponto
(c) , no ponto
(d) , com , , em um ponto genérico.
Dica: para o item (b), lembre que ; para o item (c), multiplique o numerador e o denominador por
Ver solução completaQuestão 48
Dada . Suponhamos que . Então:
- é decrescente
- , temos se
- Nenhuma das respostas acima é correta
Questão 52
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 53
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 56
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 58
Esboce gráficos e use argumentos de aproximação para calcular os seguintes limites:
Questão 60
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 61
Esboce gráficos e use argumentos de aproximação para calcular os seguintes limites:
Questão 62
Utilizando apenas as propriedades de limite, que e que , calcule . Comentário 1. Você deve estar se perguntando qual a necessidade desse exercício, já que bastava ter “trocado” x por 2. Daqui algumas aulas aprenderemos uma lista de funções em que podemos calcular limite dessa forma, apenas trocando o x. Essas funções serão chamadas de contínuas. Porém, como ainda não sabemos quem são elas, resolvemos limites com as ferramentas que temos (por enquanto, as propriedades de limites, que e que, em que e não números fixados).
Comentário 2. Imagine que um exercício com enunciado análogo ao que você acabou de fazer peça para usar as propriedades para calcular o limite . Você iria pensar: preciso fazer um monte de etapas como antes para verificar que era só substituir x por −3. Nesse pensamento, você mentalmente usou as propriedades para chegar a essa conclusão de que poderia calcular o limite apenas substituindo x. Esse é o objetivo do próximo exercício: dizer se você pode ou não resolver o limite apenas substituindo (lembre-se de pensar se as propriedades funcionam no item analisado).
Ver solução completaQuestão 68
O gráfico de uma função está esboçado a seguir
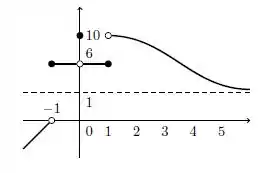
Qual das seguintes afirmações é verdadeira?
- não existe
Não é necessário justificativa.
Ver solução completaQuestão 71
2. Esboce o gráfico de um exemplo de uma função que satisfaça todas as condições dadas.
Questão 72
2. Esboce o gráfico de um exemplo de uma função que satisfaça todas as condições dadas.
b.
não está definido.
Ver solução completaQuestão 73
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 74
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 77
13. Suponha que e . Especifique quais regras do teorema abaixo utilizadas para efetuar as etapas 1, 2 e 3 do cálculo a seguir:
Teorema (Leis do Limite). Se e são números reais e
e ,
Então:
1.
2.
3.
4.
5.
6. onde
7. , onde
Ver solução completaQuestão 78
14. Suponha que , e . Especifique quais regras do teorema abaixo utilizadas para efetuar as etapas 1, 2 e 3 do cálculo a seguir:
Teorema (Leis do Limite). Se e são números reais e
e ,
Então:
1.
2.
3.
4.
5.
6. onde
7. , onde
Ver solução completaQuestão 84
Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Questão 85
Determine se cada afirmativa abaixo é sempre verdadeira, ou pode ser falsa. Justifique sua resposta.
- Pode existir sem que exista e .
Questão 86
1) Se a posição de um carro no instante é dada por , então a velocidade média entre os instantes e é dada por
Quanto mais próximo estiver de zero, mais perto a velocidade média estará da velocidade em , de modo que essa velocidade vale
Para cada função abaixo, simplifique o quociente que dá a velocidade média entre os intentes e . Em seguida, calcule a velocidade fazendo se aproximar de zero.
(a) , no ponto
(b) , no ponto
(c) , no ponto
(d) , com , , em um ponto genérico.
Dica: para o item (b), lembre que ; para o item (c), multiplique o numerador e o denominador por
Ver solução completaQuestão 90
06) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 92
07) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 93
02) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 95
03) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 99
05) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 102
08) Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Ver solução completaQuestão 104
16) Dê um exemplo com duas funções e tais que seja contínua em , seja descontínua em e, no entanto, seja contínua em .
Ver solução completaQuestão 107
Decida se a proposição abaixo é verdadeira ou falsa justificando:
Se e , então
Ver solução completaQuestão 114
5b) Sabe-se que e é definida em Todas as afirmativas abaixo são falsas. Tente desenhar um contraexemplo para cada uma delas.
Ver solução completaQuestão 117
Avalie os limites abaixo e encontre o correspondente valor caso exista. Justifique suas respostas.
Ver solução completaQuestão 129
Encontre o valor do limite indicado a seguir. E, conforme o caso, indique os Teoremas de limite usados (Propriedades Operatórias de Limites).
(c)
Ver solução completaQuestão 132
32. Dê exemplo de uma função definida em e que seja contínua em todos os pontos, exceto em
Ver solução completaQuestão 137
Encontre o ponto do gráfico de onde a reta tangente é paralela à reta
Ver solução completaQuestão 152
37. Sejam e duas funções com mesmo domínio tais que e para todo em , onde é um número real fixo. Prove que
Ver solução completaQuestão 157
Sejam tais que então:
- Teremos sempre que
- Teremos sempre que
- Podemos ter
- Teremos sempre que
- Podemos ter
Questão 158
2) Para a função definida abaixo:
a) Encontre o domínio maximal para .
b) Considerando este domínio, faz sentido estudar o limite ?
Ver solução completaQuestão 174
5c) Sabe-se que e é definida em Todas as afirmativas abaixo são falsas. Tente desenhar um contraexemplo para cada uma delas.
é positivo
Ver solução completa