A região limitada abaixo pela parábola e acima pela reta será dividida em duas subseções de área igual, sendo cortada transversalmente pela reta horizontal .
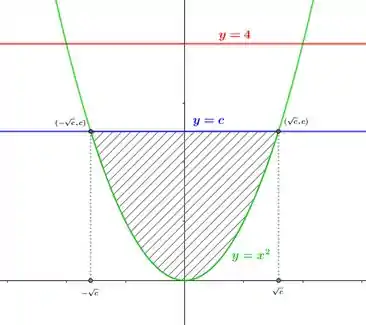
a. Esboce a região e, através dela, trace a reta , onde parecer certo. Em termos de , quais são as coordenadas dos pontos em que a reta e a parábola se cruzam? Adicione-as à figura.
Passo 1
Inicialmente esboçaremos a região que compreende a região entre limitada abaixo pela parábola e acima pela reta
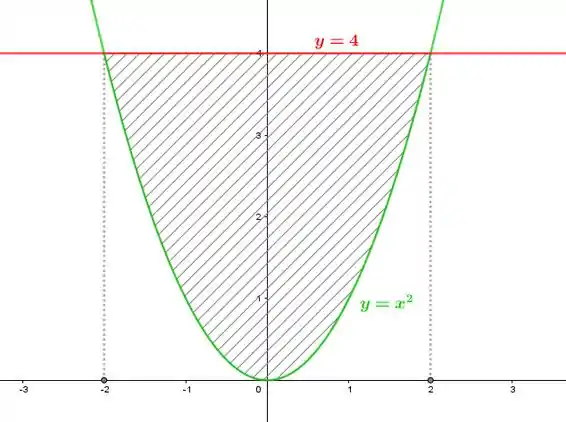
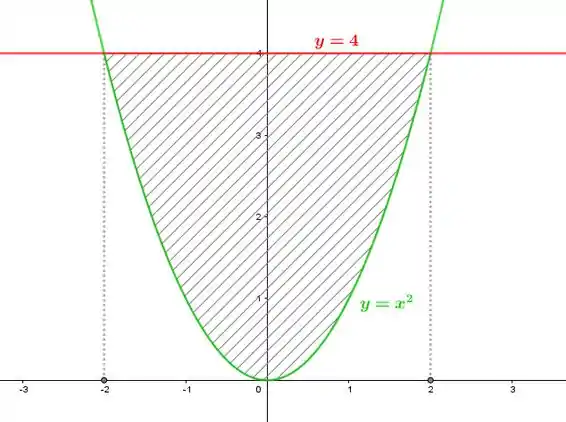 Cuja área corresponde:
Cuja área corresponde:
Passo 2
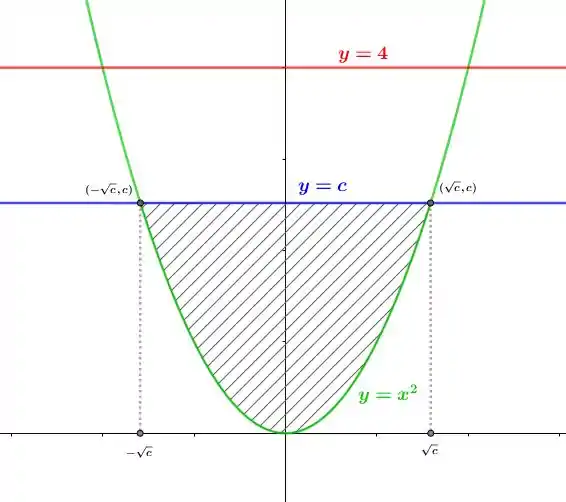
Em seguida, encontraremos a solução do item a, para isso utilizaremos as informações dadas no enunciado a respeito da reta para traça-la e determinar a sua interseção com a curva .
Sabemos que é uma reta horizontal, que divide a seção determinada interiormente em duas subseções de área igual.
Além disso, para determinar a interseção entre e precisamos que
Ou seja, a interseção entre eles são os pontos e
Sendo assim quando formos determinar a posição de , ela será da forma:
Passo 3
Nosso objetivo agora é solucionar o item b, ou seja, precisamos determinar o valor de com relação a variável , mas antes disso valor utilizar as informações que temos.
Sabemos que é uma reta horizontal, que divide a seção determinada interiormente em duas subseções de área igual, ou seja, a área da nova região que queremos calcular é igual a:
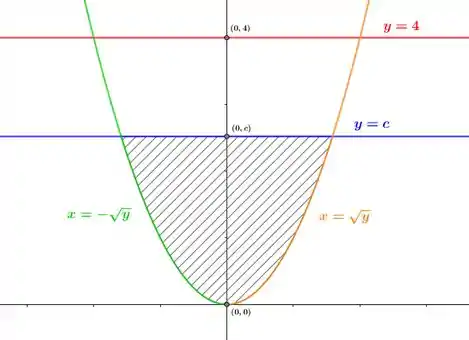
Ou seja, em relação a temos as seguintes curvas:
Onde a área que queremos calcular em relação a começa em e vai até
Logo, para determinar calcularemos a seguinte integral :
Isso, pois em relação a a integral entre área é corresponde a integral da curva da “frente “ menos a curva de “traz ”
Usando a regra de retirada da constante (integral da constante é a constante vezes a integral).
Utilizando o fato de
Usando o Teorema Fundamental do Cálculo Parte II,
Portanto,
Passo 4
Nosso objetivo agora é solucionar o item c, ou seja, precisamos determinar o valor de com relação a variável , mas antes disso valor utilizar as informações que temos.
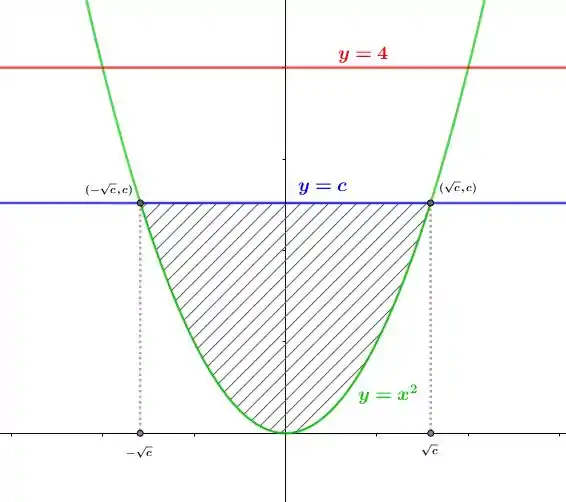
Sabemos que é uma reta horizontal, que divide a seção determinada interiormente em duas subseções de área igual, ou seja, a área da nova região que queremos calcular é igual a:
Onde a área que queremos calcular em relação a começa em e vai até
Logo, para determinar calcularemos a seguinte integral :
Isso, pois em relação a a integral entre área é corresponde a integral da curva da “cima “ menos a curva de “baixo ”
Usando o Teorema Fundamental do Cálculo Parte II,
Usando o fato
Utilizando as propriedade de potências que e
Portanto,.
Resposta
Item a. A interseção entre e são os pontos e
Item c. Em relação a .