Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 11
Uma região no plano é dada. Determine equações para a transformação que mapeia uma região retangular no plano sobre , onde os lados de são paralelos aos eixos e .
é limitado por
Passo 1
Olá pessoal, tudo bem?
Vamos entender o que essa questão quer...
Ela deu pra gente uma região no plano , que é limitada por
E quer que a gente encontre uma transformação que leve um retângulo do plano nessa região.
Como assim??
Bom, a ideia é o seguinte: se a gente pegar todos os pontos desse retângulo e aplicar a transformação, isso vai formar a região ! Isso que significa dizer que a transformação mapeia sobre .
Tá, mas como que a gente resolve isso?
Uma região retangular quer dizer que as variáveis e vão ter limites constantes:
Ou seja, os limites de uma das variáveis não dependem da outra.
Pra achar isso, vamos olhar pras equações das retas que definem , e achar duas expressões que envolvam e , e que tenham limites constantes.
Essas expressões vão ser e !
Passo 2
Pra ficar mais fácil de identificar as comparações que vamos fazer, começamos desenhando essas retas pra identificar a região :
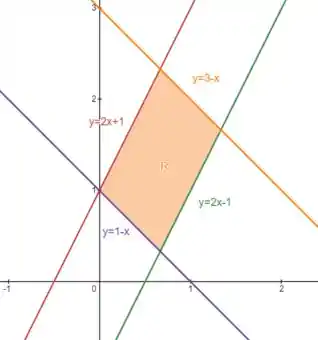
Percebe que a região é um paralelogramo, que é limitada por dois pares de retas paralelas:
E
Vamos olhar pra cada um desses pares pra achar nossas relações!
A região é um paralelogramo limitado pelas equações paralelas:
Passo 3
Começando com
Percebe que se jogarmos o pra direita, teremos uma expressão igual:
Bom, disso podemos dizer que:
E é isso que queríamos! Já temos a primeira variável:
Agora olhando para
De novo vamos jogar o e o pro mesmo lado:
Daí, temos que:
E achamos a segunda variável:
Passo 4
Então as duas variáveis são:
Que definem um retângulo no plano :
Pra finalizar, e acharmos a transformação, a gente precisa de equações desse tipo:
Dadas
Vamos fazer um sisteminha, e isolar e em função de e .
Primeiro, vamos subtrair uma equação da outra (pra sumir com o ):
Agora, vamos somar a primeira equação com o dobro da segunda (pra sumir com o ):
E achamos nossa transformação: