Seja . Faça o seguinte:
- Ache os extremos relativos de pelo teste da derivada primeira;
- Determine os valores de nos quais os extremos relativos ocorrem;
- Determine os intervalos nos quais é crescente;
- Determine os intervalos nos quais é decrescente;
- Faça um esboço do gráfico.
Passo 1
Observe que é uma função polinomial, logo é contínua e derivável para todo real. Assim, pelas regras de derivação:
Como existe para todos valores de , os pontos críticos de ocorrem quando . Assim:
Logo:
Ou:
Assim os pontos críticos de ocorrem quando ou .
Passo 2
Para determinar se tem um extremo relativo em ou devemos aplicar o teste da primeira derivada. Assim:
:
e é crescente.
:
e é decrescente.
:
e é crescente.
Logo, pelo teste da primeira derivada, em temos um ponto de máximo relativo e em temos um ponto de mínimo relativo de .
Passo 3
Observando o estudo da derivada feito anteriormente podemos fazer um esboço do gráfico de . O gráfico é dado por:
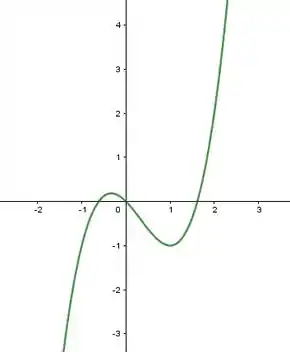
Resposta
Portanto, é crescente no intervalo e , decrescente no intervalo , admite mínimo relativo em e máximo relativo em .