Exercícios de Teste de Crescimento e Decrescimento - Lista de Exercícios Resolvida
Questão 1
Determine:
Os intervalos nos quais é crescente.
Os intervalos nos quais é decrescente.
Ver solução completaQuestão 2
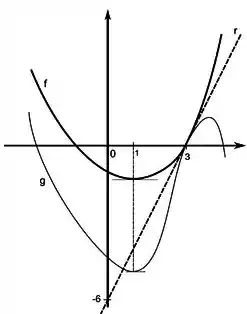
Considere e funções definidas pelos gráficos abaixo. Sabendo que é tangente ao gráfico da e ao da em , e que corta os eixos nos pontos indicados, faça um esboço, no mesmo par de eixos, do gráfico das derivadas e .
Questão 3
Dada a função , determine:
os intervalos de crescimento e decrescimento de ;
Ver solução completaQuestão 4
Seja
Determine os intervalos do domínio de onde a sua derivada seja positiva, negativa ou nula.
Ver solução completaQuestão 7
Prove a desigualdade . (Sugestão: prove para e e depois use o fato de que as funções de ambos os lados são pares)
Ver solução completaQuestão 8
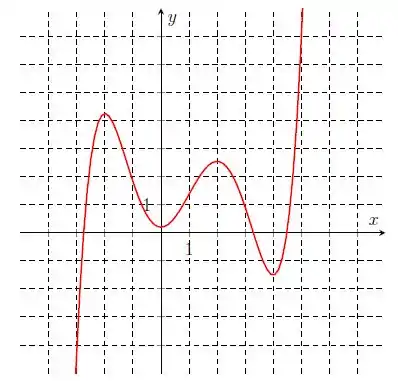
Considere a função cujo gráfico está representado abaixo. Determine os intervalos de crescimento e decrescimento de
Questão 10
Esboce, no espaço abaixo, o gráfico da função , determinando:
os intervalos de crescimento e decrescimento de ;
Ver solução completaQuestão 11
Considere uma população de cardume de peixes em certo lago, medida em centenas de milhares de peixes em t anos. Os peixes são pescados com certa frequência e dada suas taxas de reprodução, as populações evoluem de acordo com
a) Notando que , qual a população crítica que esse modelo nos fornece, ou seja, qual constante é tal que é solução da equação acima?
b) Sabendo que calcule quantos anos teremos até a extinção dos peixes neste lago, ou seja,
Ver solução completaQuestão 12
Para cada uma das funções abaixo, determine os intervalos de crescimento e decrescimento.
Questão 13
Para cada uma das funções abaixo, determine os intervalos de crescimento e decrescimento.
(b)
Ver solução completaQuestão 15
Para cada uma das funções abaixo, determine os intervalos de crescimento e decrescimento.
Ver solução completaQuestão 16
Para cada uma das funções abaixo, determine os intervalos de crescimento e decrescimento.
Ver solução completaQuestão 19
ME02) Seja dada por então:
- e é estritamente crescente
- Nenhuma das alternativas é correta
- e tem um ponto de mínimo local
- e tem um ponto de mínimo local
- e é estritamente crescente
Questão 20
Considere a função dada por:
É correto afirmar que é estritamente crescente em:
Questão 21
Considere a função dada por:
É correto afirmar que é estritamente crescente em:
Questão 22
Considere a função dada por:
É correto afirmar que é estritamente decrescente em:
Questão 23
5. Faça uma tabela de valores para a função nos pontos , , , , e .
b) Amplie a tabela, se necessário, para tentar determinar a taxa de variação de em .
Ver solução completaQuestão 24
4. Nos exercícios de a) – f), determine a taxa de variação média da função nos intervalos dados.
a) a., b.
Ver solução completaQuestão 27
Seja a função contínua e que não se anula para nenhum valor de em seu domínio. Sabe-se que:
- Prove que a função é crescente para entre .
- Determine o coeficiente angular da reta tangente ao gráfico da função no ponto .
Questão 28
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 29
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 30
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 31
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 32
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 33
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 34
Seja a função contínua e que não se anula para nenhum valor de em seu domínio. Sabe-se que:
- Prove que a função é crescente para entre .
- Determine o coeficiente angular da reta tangente ao gráfico da função no ponto .
Questão 35
Dada a função . Determine:
a) intervalos de crescimento e decrescimento e extremos locais.
Ver solução completaQuestão 36
Considere a função cuja derivada é
(b) os intervalos onde a função é crescente ou decrescente
Ver solução completaQuestão 37
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
i)
- Encontre os intervalos de crescimento e de decrescimento de .
Questão 38
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Encontre os intervalos de crescimento e de decrescimento de
Ver solução completaQuestão 39
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Encontre os intervalos de crescimento e de decrescimento de
Ver solução completaQuestão 40
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Encontre os intervalos de crescimento e de decrescimento de
Ver solução completaQuestão 43
Sejam uma constante positiva e satisfazendo:
E
- Determine os pontos críticos, intervalos em que é crescente e intervalos em que é decrescente.
- Determine e use o teste da derivada segunda para classificar os pontos críticos de
- Determine os intervalos em que a concavidade do gráfico de é para cima, os intervalos em que ela é para baixo e os pontos de inflexão do gráfico de .
- Usando os itens anteriores, faça um esboço do gráfico de supondo que
Questão 44
- Considere a dada por e suas derivadas e
- Determine os intervalos onde a função é crescente e onde é decrescente.
Ver solução completaQuestão 45
Mostre que tem exatamente uma raiz real e localize-a em um intervalo de amplitude máxima .
Ver solução completaQuestão 47
Determine os intervalos para os quais as funções seguintes são crescentes e decrescentes.
Ver solução completaQuestão 48
Determine os intervalos para os quais as funções seguintes são crescentes e decrescentes.
Ver solução completaQuestão 49
Use um recurso gráfico para determinar os intervalos de crescimento e decrescimento das funções:
.
Ver solução completaQuestão 50
Para cada uma das funçõess abaixo, determine os intervalos de crescimento e decrescimento
,
Ver solução completaQuestão 51
Para cada uma das funçõess abaixo, determine os intervalos de crescimento e decrescimento
Ver solução completaQuestão 52
Seja . Admita que .
Determinar os intervalos abertos nos quais é estritamente crescente e nos quais é estritamente decrescente;
Ver solução completaQuestão 53
Suponha que você receba uma oferta para trabalhar por apenas um mês. Qual das seguintes formas de pagamento você prefere?
Um milhão de dólares no fim do mês.
Um centavo de dólar no primeiro dia do mês, dois centavos no segundo dia, quatro centavos no terceiro dia, e em geral, centavos de dólar no n-ésimo dia.
Ver solução completaQuestão 54
Seja
(a) Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo e mínimo.
Ver solução completaQuestão 55
Seja
(a) Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo e mínimo.
Ver solução completaQuestão 59
Use um recurso gráfico para determinar os intervalos de crescimento e decrescimento das funções:
;
Ver solução completaQuestão 60
4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
b) a., b.
Ver solução completaQuestão 61
4. Nos exercícios de a) – f) , determine a taxa de variaç��o média da função nos intervalos dados.
c) a., b.
Ver solução completaQuestão 62
4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
f)
Ver solução completaQuestão 63
6. Seja para .
a) Determine a taxa de variação média de com relação a nos intervalos , e .
Ver solução completaQuestão 64
5. Faça uma tabela de valores para a função nos pontos , , , , e .
a) Determine a taxa média de variação de nos intervalos para cada em sua tabela.
Ver solução completaQuestão 65
4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
e)
Ver solução completaQuestão 66
6. Seja para .
b) Faça uma tabela de valores da taxa média de variação de com relação a no intervalo para alguns valores de que se aproximem de zero, como e .
Ver solução completaQuestão 67
7. Seja para .
a) Determine a taxa de variação média de com relação a nos intervalos
i) de a
ii) de a
Ver solução completaQuestão 68
7. Seja para .
b) Faça uma tabela de valores de taxa média de variação de com relação a no intervalo , para alguns valores de que se aproximem de 2, como e .
Ver solução completaQuestão 69
7. Seja para .
c) O que a sua tabela indica é a taxa média de variação de com relação a em ?
Ver solução completaQuestão 70
Seja
- Calcule a derivada de
- Determine a equação da reta tangente ao gráfico de em
- Determine os intervalos de crescimento e decrescimento de para
Questão 71
Considere a função dada por:
É correto afirmar que é estritamente decrescente em:
Questão 72
Faça alguns exemplos ilustrando o seguinte resultado: seja uma função contínua no intervalo .
Parte 1: Se para todo então será crescente em
Ver solução completaQuestão 73
Faça alguns exemplos ilustrando o seguinte resultado: seja uma função contínua no intervalo .
Parte 2: Se para todo então será decrescente em
Ver solução completaQuestão 76
Seja . Determine o(s) intervalos onde a função é decrescente
(a)
(b) Nenhuma das respostas
(c)
(d)
(e)
Ver solução completaQuestão 77
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
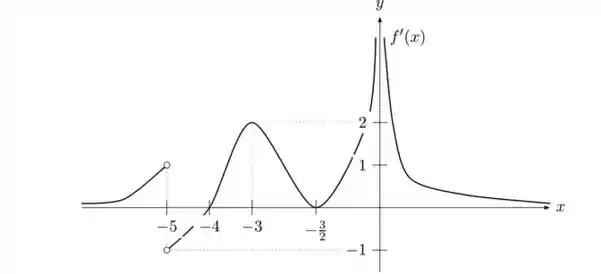
Responda, justificando, o que se pede:
Os intervalos onde é crescente, e onde é decrescente.
Ver solução completaQuestão 78
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
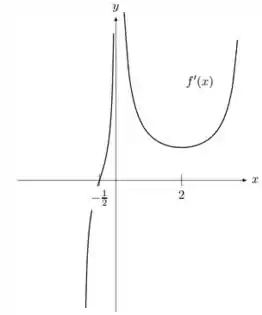
Responde o que se pede:
a) Os intervalos onde é crescente, e onde é decrescente.
Ver solução completaQuestão 86
Uma particula se desloca sobre o gráfico da fun ̧c ̃ao
no quadrante de forma que sua coordenada é o vértice de um triângulo retângulo como na figura abaixo.
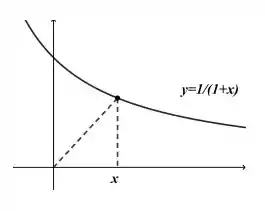
Se a taxa de variação da coordenada é constante igual a , determine a taxa de variação área do triângulo no instante em que .
Ver solução completaQuestão 89
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
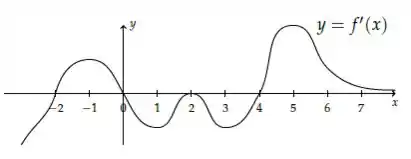
- Em que intervalos é crescente ou decrescente?
Questão 90
Para cada uma das funções abaixo, determine os intervalos de crescimento e decrescimento.
(c)
Ver solução completaQuestão 91
O gráfico da função derivada de uma função contínua é dado abaixo
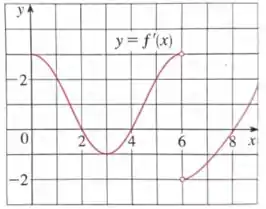
- Quais são os pontos de inflexão?
Questão 92
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Questão 93
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
b)
Ver solução completaQuestão 95
6. Seja para .
c) O que sua tabela indica é a taxa de variação de com relação a em ?
Ver solução completaQuestão 96
6. Seja para .
d) Calcule o limite, quando se aproxima de zero da taxa de variação média de com relação a no intervalo .
Ver solução completaQuestão 97
4. Nos exercícios de a) – f) , determine a taxa de variação média da função nos intervalos dados.
d) a., b.
Ver solução completaQuestão 98
Um balão esférico está sendo enchido a uma taxa de . Encontre a taxa de crescimento do raio do balão quando o diâmetro for igual a . Encontre todos os pontos sobre a curva dada pela equação
nos quais a inclinação da reta tangente à curva é igual a .
Ver solução completaQuestão 99
A altura de um objeto que se desloca verticalmente é dada por
,
com h em m e t em segundos. Determine: (a) a velocidade do objeto quando t = 0;
Ver solução completaQuestão 100
O gráfico da função derivada de uma função contínua é dado abaixo
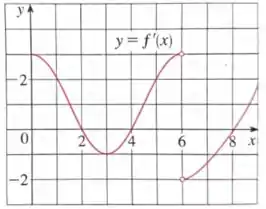
- Em que intervalos está crescendo? E decrescendo?