Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 12
Seja , , e . Desenhe a imagem de .
Passo 1
Vamos reescrever essa transformação pra ficar melhor de a gente ver:
Olha só, se fizermos , a gente obtém:
Ou seja, temos um círculo de raio . No caso, temos variando de .
O representa a altura, e o que é um círculo com altura? Um cilindro né?!
Ou seja, temos um cilindro de altura indo de .
O desenho da imagem então é:
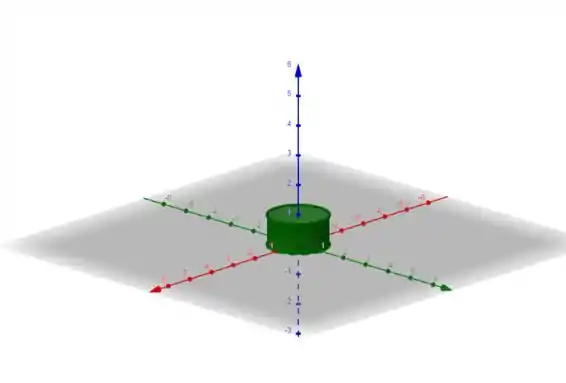
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaParte da esfera x 2 + y 2 + z 2 = 8 que está no 2 º º octante
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaCone gerado pela semi-reta z = 2 y , y ≥ 0 quando esta gira em torno do eixo positivo dos z
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaEsfera centrada na origem e raio 2
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaParte da esfera x 2 + y 2 + z 2 = 1 acima do plano z = 1 2
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaParte do cilindro x 2 + y 2 = 16 , - 2 ≤ z ≤ 2 llimitado por x = y , y ≥ 0 e x = y 2