Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 24
Seja . Prove que
a) para
b) é contínua em
Passo 1
a) Para provar que devemos desenvolver o lado esquerdo da inequação:
Se , logo , então é raiz de , assim, podemos fatorar esse polinômio, colocando em evidência:
Usando o método de Briot-Ruffini para dividir os polinômios temos:
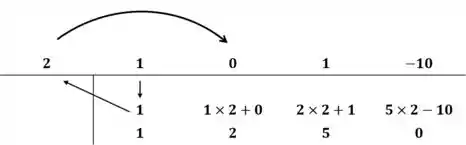
Assim:
Então:
Como não possui raízes reais e é sempre um número positivo, então:
Para um valor :
Assim,
E como podemos reescrever a inequação de modo que:
Logo, provamos que para .
Passo 2
b) Para ser contínua em , basta que para todo exista tal que para um qualquer do domínio tenhamos:
E como provamos no item (a) que para , temos , então podemos dizer que sempre vai existir para qualquer que satisfaça
Tomando :
Assim, provamos que a afirmação é verdadeira e, portanto, é contínua em .
Resposta
Ei, a resposta está no passo a passo :)