Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.5 - Ex. 19
Seja a região limitada pelas curvas e . Se for a medida da área de e for a coordenada do centróide de , prove que a medida do volume do sólido de revolução obtido ao girarmos em torno do eixo é dada por . Enunciando esta igualdade temos que:
Se uma região plana girar em torno de uma reta em seu plano que não corta a região, então, a medida do volume do sólido de revolução gerado será igual ao produto da medida da área da região pela medida da distância percorrida pelo centróide da região.
O enunciado acima é conhecido como o teoram de Pappus para volume de sólidos de revolução.
Passo 1
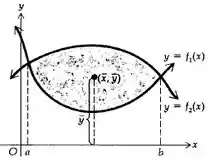
Seja R limitada por baixo por e por cima por , .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use um gráfico para encontrar as coordenadas aproximadas x dos pontos de intersecção das curvas dadas. A seguir, encontre a área aproximada da região limitada pelas curvas y = xs e nx 2 ,y = x 4
Encontrar a área da região limitada pelas curvas dadas. y = ln x ,x = 1ey = 4
Encontrar a área da região limitada pelas curvas dadas. y = 1 x + 1 ,y = 1 x ,y = 2 x + 1ex = - 3
Encontrar a área da região limitada pelas curvas dadas. y = x - 2ey = 2 - x - 2 2
Calcular a área da parte da circunferência x = 2 cos t y = 2s e nt Que está acima da reta y = 1 .