Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 14
Suponha que seja diferenciável em toda parte. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
14.Se for crescente em , e for decrescente em , então tem uma inflexão em .
Passo 1
A afirmação é falsa.
Ela deveria ter as informações extra de que, pro sinal da derivada mudar de um intervalo pro outro, no ponto em que isso acontece – no caso, – deve existir um ponto em que a derivada se anule, ou então uma descontinuidade da função.
Como nossa é diferenciável em toda parte, só poderíamos ter o caso de um ponto onde a derivada se anula – um ponto de máximo, como nossa função é crescente no intervalo , exatamente em .
Acontece que um ponto de máximo (ou também um ponto de mínimo) nem sempre é um ponto de inflexão, ou seja, nem sempre é um ponto onde a função muda de concavidade.
Passo 2
Um exemplo simples de função que ilustra isso é:
:
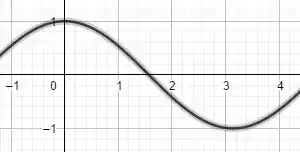
Repare o ponto de máximo em , em que o sinal da derivada muda, mas a concavidade permanece voltada pra baixo.
Isso faz com que a afirmação esteja generalizando a situação de um caso específico pra todos os casos de função com pontos em que a derivada se anule. Logo, é falsa.
Resposta
Falsa.