Suponha que seja um ponto no qual uma função seja contínua, mas não diferenciável, e que tenda a limites finitos distintos quando tende a pela esquerda e pela direita. Invente um nome para descrever o gráfico de num ponto desses e discuta a conveniência dessa sua terminologia.

Um exemplo clássico desse tipo de questão é a . É uma função contínua, porém olha o que acontece:

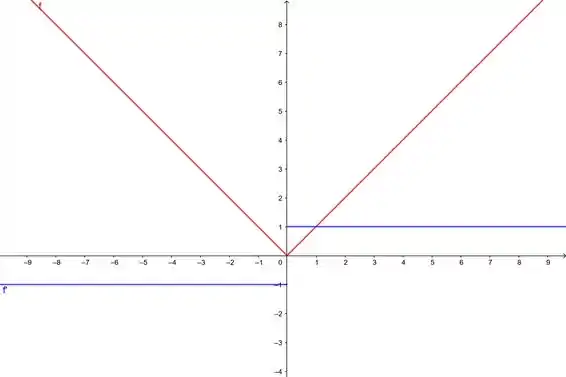
Lá no ponto ela não é derivável. Veja que nesse caso as derivadas tendendo a direita e a esquerda são:

Ou seja, são derivadas finitas e diferentes.

Dizemos que a função não é diferenciável em porque não é possível traçar uma reta tangente ao gráfico nesse ponto.

Um nome bastante usado para esses pontos (que não fui eu quem inventei 😪) é ponto de bico, porque é exatamente isso, a função faz um bico, onde não é possível existir derivada.

Em qualquer função onde é contínua porém os limites laterais da derivada são finitos e distintos, pode apostar que vai ter um ponto de bico lá.. 😉