Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.4 - Ex. 15
Use uma calculadora para isso, tanto uma função exponencial e uma função logística para esses dados. Faça um gráfico dos pontos de dados e ambas as funções, e comente a precisão dos modelos. [Dica: subtraia 94.000 de cada população figures. Depois de obter um modelo da sua calculadora, adicione 94.000 para obter seu modelo inicial. Pode ser útil escolha t = 0 para corresponder a 1960 ou 1980.]
Passo 1
Temos a seguinte tabela de dados
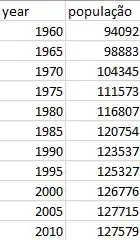
Se plotarmos esses dados teremos
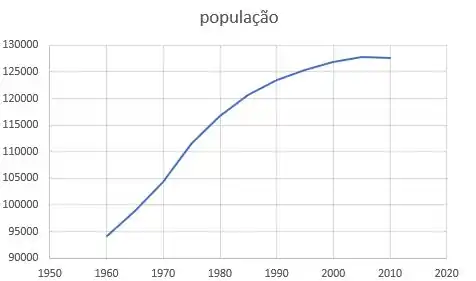
O exercício nos pede para comparar a curva de dados real com a curva formado pelo nosso modelo populacional
Precisamos então é resolver nossa equação diferencial.
O que temos aqui para resolver a questão a) é saber olhar para dados e encontrar significado. A expressão padrão para crescimento populacional é
O enunciado nos diz que podemos escrever k( medido em milhões ) como :
Assim nossa equação fica
E nosso também é medido em milhões
Passo 2
Temos que resolver essa equação diferencial e encontrar . O próprio Stewart nos dá essa solução, através de integração por partes, dizendo que
Onde
E é nossa constante arbitraria de integração indefinida. Vamos plotar os valores
Agora vamos descobrir a solução de
Sabendo que milhões (considerando o ano 2000 como nosso marco )
Então nossa função fica
Agora só nos resta fazer
milhões
Passo 3
Podemos continuar com nossa analise e predizer uma estimativa pra população dos EUA em 2200.
Ou seja, teremos
ilhões
Passo 4
Vamos calcular em que ano a população chegara em 500 milhões de habitantes
anos
Então terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
- milhões
- ilhões
- anos