Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 5
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Vamos usarmos o roteiro de esboço de curvas dado na seção para esboçar o gráfico da função dada. Teremos que achar as raízes, interseções com eixos, analisar intervalos de crescimento e decrescimento, concavidade e limites no infinito.
Passo 2
Como se trata de um polinômio, o domínio é real: .
Passo 3
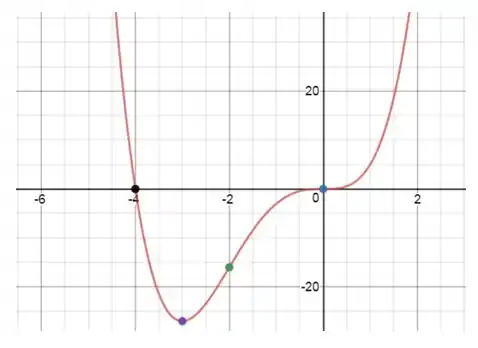
Vamos achar as interseções com os eixos e . O ponto que corta o eixo é pois quando , temos que . Para as interseções com o eixo , fazemos , assim
Assim, as raízes são e . As interseções com os eixos são e .
Passo 4
Como a função tem potencias de expoentes par e ímpar, ela não nem par nem ímpar.
Passo 5
Como é um polinômio, não tem assíntotas:
Passo 6
Para estudarmos os intervalos de crescimento e decrescimento, vamos derivar :
Como , segue que:
Assim, é um ponto crítico que não é extremo local e é ponto de mínimo local. Temos que .
Mínimo local: .
Passo 7
Para a concavidade, precisamos da segunda derivada:
Assim,
Como e os pontos e são pontos de inflexão.
Resposta
Esboço da curva:
