Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 10

Use o roteiro dessa seção para esboçar a curva.

y = x x - 1 2

Passo 1

Eaee, belezinha?? Bom... A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.

Assim, precisamos encontrar o domínio da função, interseção com eixos, limites no infinito, intervalos de crescimento, pontos críticos, fazer um estuda da concavidade e qualquer outra consideração que ajude a entender bem o comportamento da função.

Primeiro, determinamos o domínio da função

y = x x - 1 2

- A função está indefinida quando o denominador é zero.

- (   x - 1 2 =   0 ⇒   x   =   1   ) .

- Portanto, o domínio da função é (   x ∈ R   { 1 } ) .

Passo 2

Analisamos as assíntotas verticais e horizontais.

- Assíntota Vertical:

- Ocorre quando o denominador se aproxima de zero, ou seja, em x = 1 .

- Portanto, há uma assíntota vertical em x = 1 .

- Assíntota Horizontal:

- Para encontrar assíntotas horizontais, analisamos o comportamento da função quando (   x ��   ∞   )   e   (   x →   - ∞   ) .

y = x x - 1 2

- Para (   x →   ∞   ) :

        y   ≈ x x 2 = 1 x → 0

- Para (   x → -   ∞   ) :

        y   ≈ x x 2 = 1 x → 0

- Portanto, há uma assíntota horizontal em ( y = 00 .

Passo 3

Calculamos a derivada para entender o comportamento monótono da função.

y = x x - 1 2

Usamos a regra do quociente para derivar:

d y d x = x - 1 2 ⋅ 1 - x ⋅ 2 x - 1 x - 1 4

d y d x = x - 1 2 - 2 x x - 1 x - 1 4

d y d x = x 3 - 2 x + 1 - 2 x 4 + 2 x x - 1 4

d y d x = - x 2 + 1 x - 1 4

d y d x = - x 2 - 1 x - 1 4

d y d x = - x - 1 x + 1 x - 1 4

d y d x = - x + 1 x - 1 3

Passo 4

Analisamos os pontos críticos onde d y d x = 0 :

- ( x + 1 )   =   0

  x   =   - 1  

Analisamos o sinal da derivada em torno deste ponto crítico e da assíntota vertical em x = 1 :

- Para (   x   <   - 1   ) :

d y d x = - ( x + 1 ) x - 1 3   ( p o r q u e   o   n u m e r a d o r   é   n e g a t i v o   e   o   d e n o m i n a d o r   é   n e g a t i v o )

A função é crescente.

- Para (   - 1   <   x   <   1   ) :

d y d x = - x + 1 x - 1 3 < 0     ( p o r q u e   o   n u m e r a d o r   é   p o s i t i v o   e   o   d e n o m i n a d o r   é   n e g a t i v o )

A função é decrescente.

- Para (   x   >   1   ) :

  d y d x = - x + 1 x - 1 3 < 0 ( p o r q u e   o   n u m e r a d o r   é   n e g a t i v o   e   o   d e n o m i n a d o r   é   p o s i t i v o )

A função é decrescente.

Portanto:

- (   x   =   - 1   ) é um ponto de máximo local.

- A função é crescente para (   x   <   - 1 )   e decrescente para (   - 1   <   x   <   1   ) .

- A função é decrescente para (   x   >   1   ) .

Passo 5

Calculamos y   quando (   x   =   0   ) :

  y 0 = 0 0 - 1 2 = 0

Calculamos o valor da função no ponto de máximo local (   x   =   - 1   ) :

y - 1 = - 1 - 1 - 1 2

= - 1 4

= - 1 4

- A função tem uma assíntota vertical em (   x   =   1   ) .

- A função tem uma assíntota horizontal em (   y   =   0   ) .

- A função é crescente para   (   x   <   - 1   ) ,   decrescente para (   - 1   <   x   <   1   ) , e decrescente para (   x   >   1   ) .

- Máximo local em (   x   =   - 1   )   com - 1 4 .

- Interseção com o eixo y em 0,0 .

Passo 6

Pontos para Esboço

- \( (0, 0) \)

- - 1 4

- Assíntota vertical em (   x   =   1 )

- Assíntota horizontal em (   y   =   0   )

Com base nas análises acima, podemos esboçar a curva da função

y = x x - 1 2

1. A função tem um máximo local em ( 1 ,   - 1 / 4 )

2. A função é crescente para (   x   <   - 1   ) e decrescente para (   - 1   <   x   <   1   ) .

3. A função cruza o eixo y em 0,0 .

4. A função tende a (   ∞   ) à medida que x se aproxima de 1   pela esquerda e tende a (   - ∞ ) à medida que ( x ) se aproxima de 1 pela direita.

5. A função tende a 0 à medida que (   x →   ∞   )   e   (   x →   - ∞ ) .

O gráfico da função será assim:

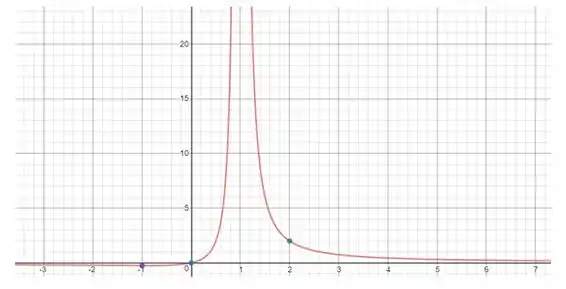
Os pontos chave ( 0,0 ) e - 1   ,   - 1 4 ajudam a definir a forma geral da curva, enquanto as assíntotas verticais e horizontais orientam o comportamento da função em extremos.

Resposta

Vide o passo a passo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Conforme mostra a figura a seguir, suponha que um barco entre em um rio no ponto ( 1 ,0 ) e mantenha sua direção voltada para a origem. Como resultado da forte corrente, ele segue a trajetória onde x
Suponha que a função posição de uma partícula em movimento retilíneo seja dada pela fórmula s t = t 2 + 1 t 4 + 1 , t ≥ 0 (a) Use um CAS para encontrar fórmulas simplificadas para a velocidade v ( t )
Use um sistema de computação algébrica para fazer o gráfico de f e encontrar f ' e f ' ' . Utilize os gráficos dessas derivadas para estimar os intervalos de crescimento e decrescimento, valores extre
O gráfico mostrado corresponde ao da função população P ( t ) de cultura em laboratório de células de levedo. Use o método do Exemplo 1 para obter o gráfico da derivada P ’ ( t ) . O que o gráfico de
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf