Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.5 - Ex. 21
Use o roteiro desta seção para esboçar a curva
Passo 1
Oieee, bora resolver mais uma junto comigo?
Primeiro, determinamos o domínio da função
- O domínio é o conjunto de valores de para os quais a função está definida.
- Como é definido para todos os reais (pois é sempre positivo e a raiz quadrada de um número positivo é sempre real), o domínio da função é todos os números reais .
Vamos verificar a simetria da função pode simplificar o esboço da curva.
- A função não é par nem ímpar. Para verificar isso:
- Uma função é par se
- Uma função é ímpar se .
Verificamos:
Isso não é igual a nem a então a função não é par nem ímpar.
Passo 2
Analisamos o comportamento da função para valores extremos de (quando e ).
- Para :
Aproximamos para valores grandes de
Portanto:
Então, quando .
- Para :
Similarmente, temos:
Então, quando .
Passo 3
Calculamos a derivada para entender o comportamento monótono da função.
Analisamos os pontos críticos onde
Essa equação não tem solução real, indicando que a derivada nunca é zero.
Analisamos o sinal da derivada:
- Para
A função é decrescente.
- Para
A função também é decrescente.
A função é estritamente decrescente em todo o seu domínio.
Passo 4
Calculamos quando
- A função tem um domínio em todos os números reais.
- A função não é simétrica.
- A função se aproxima de 0 tanto para quanto para .
- A função é estritamente decrescente.
- Interseção com o eixo y em .
Com essas informações, podemos esboçar a curva.
A curva começa em e decresce gradualmente, aproximando-se de 0 à medida que se afasta para ambos os lados
- No eixo temos o ponto
- À medida que aumenta positivamente ou negativamente, se aproxima de 0.
Um gráfico pode ser esboçado com base nessas análises.
A curva seria algo assim:
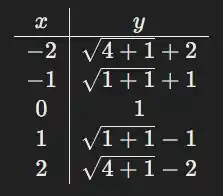
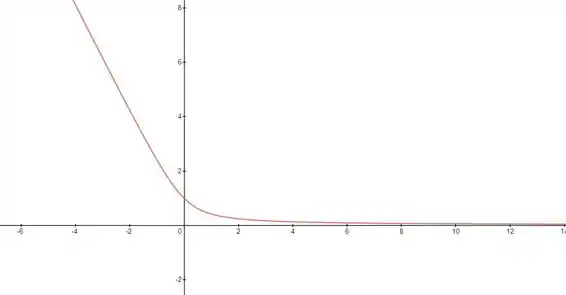
O esboço exibe uma função que desce rapidamente de para e depois lentamente se aproxima de para grandes valores de positivos e negativos.
Resposta
Vide o passoa a passo.