Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.8 - Ex. 5
Use o Teorema de Stokes para calcular
consiste no topo e nas quatro laterais (mas não o fundo) do cubo com vértices , orientada para fora.
Passo 1
Faaala minha turma, beleza!?
Precisamos usar o Teorema de Stokes para calcular:
Onde,
consiste no topo e nas quatro laterais (mas não o fundo) do cubo com vértices , orientada para fora.
Pessoal, o Teorema de Stokes é dada por:
Onde, é o rot(rotacional). Desse jeito:
A fronteira da superfície e a face do fundo do cubo são a mesma. Assim, pelo Teorema de Stokes nós podemos dizer que
onde é a superfície, é o fundo do cubo e o é a fronteira comum, que é o plano .
Importante lembrar que o rotacional é expresso por:
Onde saem do campo :
E que , pode ser representado como:
Ao invés de calcular a integral de linha de , que não é suave e consiste de quatro segmentos de reta, nós vamos calcular a integral de superfície através do fundo do cubo. O fundo deve ser orientado para cima.
Mas por que? O Teorema de Stokes e a regra da mão direita nos diz que é orientada no sentido anti-horário. Novamente, o Teorema de Stokes e a regra da mão direita nos diz que é orientada para cima porque é orientada no sentido anti-horário.
Agora já conseguimos montar a integral!
Vamos nessa!
Passo 2
Aplicando o Teorema de Stokes, temos:
Sabemos que:
Também pode ser representado como:
Porque o vetor normal aponta na direção ? Lembra que estamos calculando a integral de superfície através do fundo do cubo. E pela regra de Stokes, deve ser sentido anti-horário, e isso gera o vetor normal apontando para cima.
E sabemos que o rotacional é:
Onde,
Portanto, substituindo na integral ficamos com:
Passo 3
Fazendo o produto escalar, vamos ter:
Dado que o campo vetorial é:
Temos que as derivadas parciais são:
Assim, a integral fica:
Para todos os pontos na superfície sabemos que .
Logo, ficamos com a seguinte integral:
Passo 4
Sabemos que , pode ser escrito como:
Mas já vimos, que estamos no plano . Ele não depende de e , logo as derivadas são zero.
Assim, temos:
Como esse cubo está centrado na origem, temos os intervalos de x e y são:
Veja a figura a baixo:
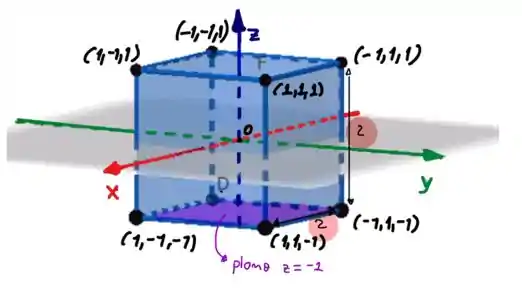
Substituindo o valor na integral, temos que:
Passo 5
Agora vamos integrar.
Lembrando que começamos a integrar de dentro para fora. Mas observe que os limites de integração são iguais e numerais, então nesse caso tanto faz a ordem que iriamos começar.
Mas vamos começar integrando em . Integrando, vamos ter:
Aplicando os limites de integração, temos:
Resolvendo, vamos ter:
Agora temos uma integral simples em .
Integrando em , ficamos com:
Aplicando os limites de integração temos:
Logo, concluímos que o resultado da integral pelo Teorema de Stokes é: