Use o Teorema de Stokes para calcular ∫ C F ∙ d r . Em cada caso, C é orientada no sentido anti-horário como visto acima. F x , y , z = x y i + ( y z ) j + ( z x ) k C é a fronteira de parte do paraboloide z = 1 - x 2 - y 2 no primeiro octante.

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.8 - Ex. 9

Use o Teorema de Stokes para calcular Em cada caso, é orientada no sentido anti-horário como visto acima.

é a fronteira de parte do paraboloide no primeiro octante.

Passo 1

E aiii minha galera fera, tudo bem com vocês!? Vamos nessa então!

Precisamos usa o Teorema de Stokes para calcular a integral de linha a seguir:

Onde,

é a fronteira de parte do paraboloide no primeiro octante.

Vamos pensar em uma estratégia juntos!

Pessoal, o Teorema de Stokes é dada por:

onde é a curva fechada que forma a fronteira, simples, suave por partes e com orientação positiva.

Por definição, o rotacional é representado como:

Onde, .

Assim, temos:

Mas sabemos também se a superfície é da forma e é orientada para cima, podemos usar a seguinte fórmula:

Aqui, vamos tomar cuidado ao substituir os valores de . Vamos colocar os valores obtidos do rotacional de .

Sabemos que faz parte do plano e que é a projeção da superfície no plano . Veja a figura abaixo:

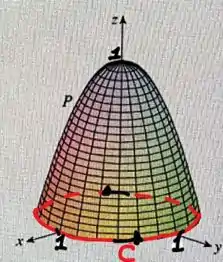
Observe que vai ser mais fácil por esse caminho, basta aplicarmos as derivadas de . Depois vamos converter tudo para coordenadas polares, pois temos um círculo no plano . Ficando assim:

Com,

Agora vou deixar com vocês os demais passos! É só organizar e aplicar na integral!

Vamos nessa!

Passo 2

Sabemos que o Teorema de Stokes é escrito como:

Tambem sabemos que é:

Onde, .

Logo, vamos ter que:

E que o rotacional de é:

Aplicando as derivadas, vamos ter que o rotacional vale:

Assim, a integral fica:

Observe que podemos comparar essa integral com a seguinte:

Assim, concluímos que:

Passo 3

Sabemos que faz parte do plano e que é a projeção da superfície no plano . Veja a figura abaixo:

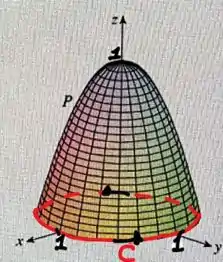
Avaliando nossa região, temos que:

Logo, as derivadas vão ser:

Substituindo na integral, vamos ter:

Simplificando, vamos ter:

Substituindo, . Vamos ter

Como vai ser a região dentro do círculo no primeiro quadrante.

Vamos passar aqui as variáveis para coordenadas polares, para facilitar nossa vida!

Com,

Assim, nossa integral vai ficar:

Passo 4

Agora podemos começar a integrar. Lembrando que começamos de dentro para fora.

Integrando em , vamos ter:

Aplicando os limites de integração, temos:

Integrando em , ficamos com:

Aplicando os limites de integração, vamos ter:

Fazendo a soma dos termos, concluímos que pelo teorema de Stokes a integral de linha vale:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. b )F → x , y , z = y i → - x 2 j → + 5 k → ,σ u , v = u , v , 1 - u 2 , c o mu ≥ 0 ,v ≥

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. d )F → x , y , z = y i → + x 2 j → + z k → ,σ é a superfície x 2 + y 2 = 1 ,0z1 ,ey ≥0

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. f )F → x , y , z = y i → ,σ é a superfície z =x 2 + y 2c o mz ≤ 1 sendo n → a normal co

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. i )F → x , y , z = - y 2 i → + x 2 j → + z 2 k → ,σ é a superfície x 2 + y 2 4 + z 2 =

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. h )F → x , y , z = - y i → + x j → + x 2 k → ,σ é a superfície x 2 + y 2 + z 2 = 4 ,2 ≤