Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.2 - Ex. 26
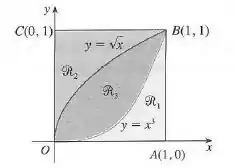
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada.
Passo 1
Bom galera, nessa questão queremos encontrar o volume do sólido gerado ao rotacionar a função apresentada em torno do eixo especificado. Para isso, utilizaremos o conceito de Volume de Sólidos de revolução e as técnicas de integração para calcular o valor desse volume.
Passo 2
Podemos escrever a seguinte integral com base em
Passo 3
Resolvendo a integral, temos
Resposta
Exercícios de Livros Relacionados
13. Determine o volume do sólido gerado pela rotação da região limitada pela curva x = e y 2 e pelas retas y = 0 , x = 0 e y = 1 em torno do eixo x .
A região entre a curva y = 1 / x 2 e o eixo x de x = 1 / 2 a x = 2 é girada em torno do eixo y , gerando um sólido. Determine o volume do sólido.
No Exercício 6 da Seção 6.2, giramos em torno do eixo y a região entre a curva y = 9 x / x 3 + 9 e o eixo x de x = 0 a x = 3 para gerar um sólido de volume 36 π . Em vez disso, se girarmos a região em
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo y . A região é a região, no primeiro quadrante, limitada à esquerda pelo círculo x 2 + y 2 = 3 , à direita pela reta x
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo y . A região é a região limitada pelo triângulo com vértices 0,1 , 1,0 e 1,1 .