Regra de três simples e composta

E aí, você acaba de chegar no Responde Aí, onde vamos tirar todas as suas dúvidas sobre Regra de três simples e composta.

A regra de três é a proporção entre dois (ou mais valores). Esse é um método universal para a resolução de diversos problemas dos mais simples aos mais difíceis.

A regra de três é uma forma de descobrir um novo valor com base em outros três valores que você já conhece (daí o nome, regra de três).

Regra de três simples e direta

Esse modelo de regra de três é aquele em que as grandezas são diretamente proporcionais e em que temos 3 informações e queremos descobrir a quarta, que será a nossa incógnita.

Duas grandezas são proporcionais se elas aumentam juntas. Por exemplo, se você aumentar o volume de água numa jarra, então o peso também aumenta. Isso acontece pois massa e volume são proporcionais.

Exemplo: Um veículo percorre uma distância de em um tempo de . Quantos segundos o mesmo veículo leva para percorrer ?

Passo 1: Primeiro, a gente precisa saber se as grandezas são diretamente proporcionais. Para isso, é só a gente pensar: “Se eu aumentar a distância, o tempo aumenta também?” Se a resposta for “sim” então as grandezas são diretamente proporcionais.

Nesse caso distância e tempo são diretamente proporcionais.

Passo 2: Agora vamos montar a nossa regra de três. Pra isso, a gente relaciona as informações:

Na questão diz que para andar eu levo segundos:

Então para andar eu levo um tempo desconhecido, que podemos chamar de

E a gente coloca isso numa expressão só:

Passo 3: Agora que está tudo montado a gente efetua uma multiplicação cruzada, que basicamente quer dizer que a gente multiplica os valores em diagonal.

Fazemos uma multiplicação cruzada, a gente multiplica vezes o que queremos descobrir, e igualamos a multiplicação de vezes :

E agora é só resolver a equação para encontrar o valor de

Pra saber mais, olha aqui esse vídeo sobre regra de três.

Regra de Três Simples e Inversa

Esse modelo de regra de três é aquele em que as grandezas são inversamente proporcionais.

Duas grandezas são inversamente proporcionais se uma aumenta enquanto a outra diminui. Por exemplo, se a velocidade de um carro aumenta, então o tempo de viagem diminui. Isso ocorre pois velocidade e tempo são inversamente proporcionais.

Exemplo: Um carro com velocidade percorre uma certa distância em . Quanto tempo levaria se viajasse a

Passo 1: Bom se a distância é a mesma e nós aumentamos a velocidade, então esperamos logicamente que o tempo vá diminuir. Então as grandezas se comportaram de maneira inversamente proporcional.

Então montaríamos nossa regra de três da seguinte forma:

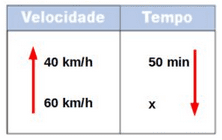
Porém antes de multiplicar cruzado, por termos reparado esse comportamento inversamente proporcional, precisamos inverter um dos lados da grandeza, no caso vou inverter o lado das grandezas do tempo:

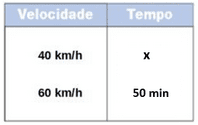
Passo 2: E agora sim podemos multiplicar cruzado para resolver a questão:

Isolando o :

Regra de Três Composta

A regra de três composta precisa ser utilizada quando lidamos com problemas que envolvem mais de duas grandezas, que podem se relacionar de maneira direta ou indireta.

Exemplo: Em horas, caminhões são capazes de descarregar sacos de cimento, quantos caminhões serão necessários para descarregar sacos de cimento em horas?

Passo 1: Primeiro precisamos notar quais grandezas estão envolvidas: tempo para descarregar, a quantidade de caminhões e o número de sacos a serem descarregados

Para aplicar a regra de três composta, primeiro montamos uma tabela com os valores que sabemos de cada grandeza e com nossa incógnita e além disso colocamos uma seta (para cima ou para baixo) na grandeza que contém a incógnita, dessa forma:

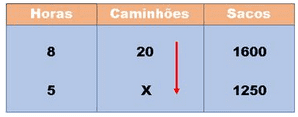
Passo 2: Depois precisamos analisar se as outras grandezas e verificar se são diretas ou inversas em relação a incógnita.

Se eu aumentar o número de caminhões, o tempo para descarregar aumenta? NÃO! Então o tempo e o número de caminhões são inversamente proporcionais.

Agora, se eu aumentar o número de caminhões, a quantidade de sacos aumenta? SIM! Então são grandezas o número de sacos e o número de caminhões diretamente proporcionais.

Então podemos completar a tabela:

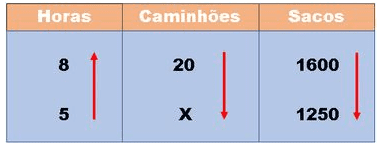
E agora, precisamos inverter a ordem da grandeza que é inversamente proporcional:

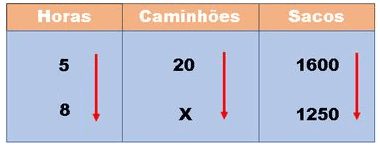
Passo 3: Agora podemos montar a equação da regra de três composta. Devemos manter a grandeza da incógnita de um lado, e multiplicar as outras duas grandezas:

Isolando o vamos ter:

Logo precisaríamos de 25 caminhões para descarregar 1250 sacos de cimento em 5 horas.

Beleza! Agora é só partir pros exercícios pra não ficar nenhuma dúvida 👇