Introdução à potenciação
Produzido por Marcelo LuizTeoria
Introdução
Faala galerinhaa, tudo bem com vocês?
A partir de agora vamos entrar no universo das potências hehe. Só pra vocês terem uma ideia, quando a potenciação foi criada, ela foi vista como uma forma mais econômica de se representar números muito grandes.
Por exemplo:
Essa multiplicação pode ser vista, como:
Por isso às vezes é muito mais prático usarmos essa forma exponencial (, do que termos o mesmo número se multiplicando diversas vezes.
Definição
Uma potência nada mais é que pegarmos um número “A” e multiplicar ele mesmo quantas vezes precisarmos (“N” vezes). Assim teremos:

Chamamos “A” de base e “N” de expoente.
E lemos:
“A elevado à N (forma ordinal) potência”
A forma ordinal é: Primeira (1), quarta (4), Quinta (5),...
Só que, nas potencias quando elevamos a expoente 3 chamamos de cubo e quando elevamos ao expoente 2 chamamos de quadrado.
Exemplo:
Lemos 7 elevado ao quadrado
Lemos 5 elevado ao cubo
Lemos 2 elevado à sétima potência
Cuidado!!!
A potênciação multiplica a base o número de vezes do expoente. Sobre nenhuma hipótese ela vai pegar a base e multiplicar pelo expoente. Ou seja :

Propriedades
- Qualquer número elevado a 1 é ele mesmo :
- Qualquer número, diferente de 0, elevado ao expoente 0 é 1 :
- 1 elevado á qualquer expoente, é 1:
- Quando temos expoente negativo, invertemos a fração (lembrando que todo número inteiro pode ser escrito como uma fração, colocando o número 1 embaixo):
- Quando elevamos uma potencia á uma potencia, nós multiplicamos os expoentes:
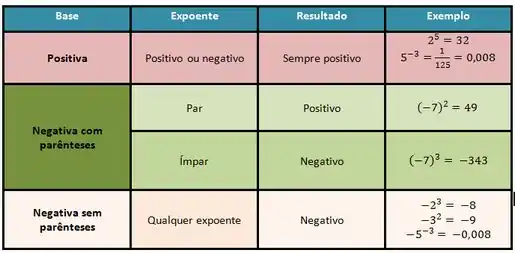
Ideias importantes
Aqui no final eu vou deixar umas dicas que pode te salvar mais pra frente, beleza? Se liga:
Prontinho, agora é só dar aquela treinada nos exercícios