Multiplicação e Divisão de Potências
Produzido por Marcelo LuizTeoria
E aí, você chegou no Responde Aí! Vamos lá aprender como fazer multiplicação e divisão de potências.
Você já conhece as potências! Por exemplo, se a gente tem a expressão
Quando se trata de multiplicação e divisão de potências a forma mais direta é: primeiro resolver as potenciações, e depois resolver as multiplicações e divisões.
Exemplo: Calcule
Porém, existem algumas regrinhas que facilitam a multiplicação e a divisão de potências quando às duas potências tem base igual ou se o expoente é igual.

Pra entender melhor essas regras é só continuar lendo
Multiplicação de potências
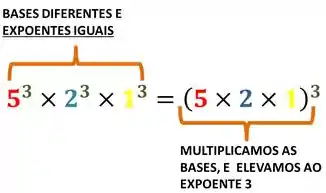
Expoentes iguais
Quando temos duas potências com o mesmo expoente, a gente pode multiplicar as bases primeiro, e depois aplicar o expoente:
Exemplo: Calcule
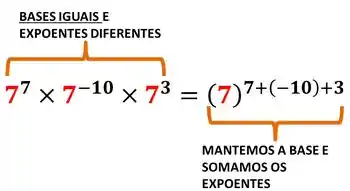
Bases iguais
A regra é simples: quando multiplicamos potências com a mesma base, a gente repete a base e soma os expoentes:
Exemplo: Calcule
Divisão de potências
Expoentes iguais
Aqui a regra é a mesma que a usada para a multiplicação, a gente pode dividir primeiro as bases e depois calcular a potenciação do resultado.
Exemplo: Calcule
Bases iguais
Aqui a regra também é bem parecida com a multiplicação. Quando dividimos potências com a mesma base, a gente repete a base e subtraímos os expoentes:
Exemplo: Calcule
E é só isso! Pra saber mais, da uma olhada nesse vídeo:
Multiplicação de potências
Divisão de potências
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Resolva:
Passo 1
Nesse caso, não temos bases e nem expoentes iguais. Por isso vamos resolver cada potenciação individualmente, depois substituímos os valores e fazemos as continhas.
Primeira:
Temos como base o número três, agora vamos multiplicar ele mesmo 6 vezes, que é o nosso expoente.
Assim:
Passo 2
Vamos resolver a segunda potenciação:
Pelas propriedades, todo número elevado á 1 é ele mesmo, assim:
Passo 3
Terceira potenciação:
Nossa base agora é o 9, como o expoente é 3, vamos multiplicar ele mesmo três vezes.
Passo 4
Agora é só substituirmos o valor que encontramos para cada uma das potências:
Agora vamos resolver a conta normalmente, podemos considerar o 729 do denominador como sendo multiplicado por um, por que isso não afeta o valor da nossa conta:
Agora, podemos transformar isso em duas frações se multiplicando, e resolver normalmente cada uma:
Resposta
5
Exercício Resolvido #2
Elaboração própria
Resolva as multiplicações:
Passo 1
- Nesse caso temos expoentes iguais, assim, a regrinha diz que podemos multiplicar todas as bases e elevar ao expoente comum:
- Agora temos bases iguais, porém expoentes diferentes, assim a regra diz que vamos manter a base e somar os expoentes.
Vamos fazer essa multiplicaçãozinha, e depois fazemos a potenciação:
Nossa base agora é o 10, por isso vamos multiplicar ele mesmo 3 vezes (expoente).
Assim, temos:
Passo 2
Vamos fazer as soma dos expoentes e resolver a potenciação:
Lembrando que uma das propriedades da potenciação diz que qualquer número elevado à zero é 1.
Assim,
Resposta
- 1000
- 1
Exercício Resolvido #3
Elaboração própria.
Resolva as divisões:
Passo 1
Belezinha! Para começar, como nós temos um expoente negativo, vamos inverter a fração e considerar o expoente como positivo:
Agora, vamos usar nossa regrinha, quando temos uma fração elevada a um expoente, podemos elevar o numerador e denominador separadamente pelo expoente na qual a fração inteira era elevada:
Sendo assim, vamos resolver as potenciações individualmente.
Começando pelo numerador, devemos lembrar que o 5 é a nossa base e ele vai ser multiplicado 3 vezes, assim:
Para a segunda potenciação (denominador), basta apenas pegarmos a base 2 e multiplicar ela mesma 3 vezes, fazendo isso teremos:
Assim, ficamos com:
Como a divisão não é exata, vamos deixar ela assim mesmo, só se pedir o resultado em decimal vamos fazê-la. Nesse caso não é necessário.
Passo 2
Agora, como temos bases iguais, vamos usar outra regrinha.
Se temos bases iguais, mantemos elas e subtraímos os expoentes, ou seja:
Note que mantemos a base 15 e fizemos a subtração dos expoentes normalmente, agora é só resolver a potenciação:
Prontinho, ficamos então com:
Resposta
a)
b)
Exercício Resolvido #4
DANTE, Luiz Roberto. Tudo é matemática -9°ano. São Paulo, SP: Ática, 2009. pp.22 (Adaptado)
Calcule o valor da expressão numérica
Passo 1
Vamos primeiramente mexer com o numerador e depois com o denominador da nossa fração, feito isso vamos substituir os valores e resolver a divisão.
Passo 2
Numerador:
Nesse caso, temos tanto as bases como os expoentes iguais, logo podemos usar qualquer uma das regrinhas.
Vamos usar a das bases iguais, relembrando de que quando temos bases iguais, a mantemos e somamos expoentes, assim ficamos:
Pronto, vamos deixar nosso numerador assim por enquanto.
Passo 3
Agora vamos mexer com o denominador:
Vamos usar novamente a regrinha das bases iguais, vamos manter a base 3, e somar os expoentes:
Deixaremos o denominador assim por enquanto.
Passo 4
Reduzimos o numerador e o denominador á uma única potência, ou seja, ficamos com:
Dá uma olhadinha nessa fração, temos bases iguais, logo para resolver vamos manter a base 3 e DIMINUIR os expoentes (cuidado para não somar os expoentes, você soma apenas na multiplicação de bases iguais), assim temos:
Todo número elevado á 1 é ele mesmo, assim temos:
Resposta
Exercício Resolvido #5
LONGEN, Adilson. Matemática em movimento 8ª Serie. Curitiba, PR: Nova Didática, 2004. pp.14 (Adaptado)
A medida do lado do quadrado abaixo é representada pela letra x.
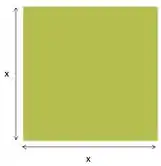
Utilize a potenciação para expressar a área do quadrado
Passo 1
Para resolvermos esse exercício, precisamos lembrar que a área de um quadrado é lado vezes lado.
Nesse caso, nosso lado vale x, por isso nossa área fica:
Passo 2
Para resolver essa multiplicação, temos bases iguais, assim mantemos a base x e somamos os expoentes (lembrando que quando não temos nenhum expoente explícito consideramos 1).
Ou seja, a área é representada por (x ao QUADRADO), interessante que foi por causa da forma geométrica que o expoente 2 ficou conhecido como quadrado.
Resposta
Exercício Resolvido #6
LONGEN, Adilson. Matemática em movimento 8ª Serie. Curitiba, PR: Nova Didática, 2004. pp.15 (Adaptado)
A medida da aresta do cubo abaixo é representada pela letra y
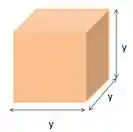
Represente o volume desse sólido pela potenciação.
Passo 1
Relembrando,
O volume do cubo é:
E todos esses valores estão sendo representados pelo valor y, assim temos:
Passo 2
Para resolvermos essa multiplicação, note que temos bases iguais, assim vamos mantê-la e basta somar os expoentes (como não tem nenhum expoente explicito, usamos o 1).
Assim temos que o volume é dado por (elevado ao cubo). Mais uma vez é interessante saber que foi por causa da figura geométrica que o expoente 3, ficou conhecido como CUBO.
Resposta
Exercício Resolvido #7
SILVEIRA, Ênio; MARQUES, Cláudio. Matemática. São Paulo, SP: Moderna, 1995. pp.8 ( Adaptado)
Utilizando as propriedades das potências, calcule:
Passo 1
Antes de resolver o exercício, vamos relembrar como fazemos multiplicação e divisão de potências com a mesma base!
No caso de uma multiplicação de potências com a mesma base, nós repetimos a base e somamos os expoentes, como no exemplo a abaixo:
Já em uma divisão de potências com a mesma base, nós repetimos a base e subtraímos os expoentes, como no exemplo a abaixo:
Note que sempre mantemos a base .
Passo 2
a)
Dá uma olhadinha, nesse caso temos a mesma base tanto no numerador quanto no denominador. Assim, para resolvermos essa divisão, vamos manter a base e subtrair os expoentes:
Note que mantemos a base e subtraímos os expoentes normalmente.
Passo 3
b)
Seguindo a mesma ideia, continuamos tendo uma base igual, só que dessa vez ela é . Sendo assim, agora é só mantermos a base e subtrairmos os expoentes, com isso teremos:
Resposta
a)
b)
Exercício Resolvido #8
SILVEIRA, Ênio; MARQUES, Cláudio. Matemática. São Paulo, SP: Moderna, 1995. pp.8
Mostre que:
Sendo
Passo 1
Geeente, esse exercício não é um monstro de 7 cabeças que parece. Você vai ver que se você pega a ideia inicial ele fica bem facinho. A gente precisa apenas dar uma mexida na função.
Se olharmos para essa expressão, podemos ver que temos dos dois lados.
Então o mais legal que poderíamos fazer agora é dividir os dois lados dessa igualdade por , assim ficaríamos só com números .
Dividindo os dois lados por , ficamos com:
Agora, vamos mexer com cada lado de uma vez e depois igualamos.
Passo 2
Vamos focar na parte da direita e simplificar:
Podemos escrever como a soma de duas frações:
Temos duas divisões com a base iguais, assim vamos manter a base de cada uma e diminuir os expoentes, assim ficamos:
Sabendo que todo número elevado a 0 é 1, e todo número elevado a 1 é ele mesmo, temos:
Ou seja,
Passo 3
Agora, vamos simplificar o segundo lado da equação:
Podemos fazer essa fação, como duas se multiplicando, assim temos:
Já descobrimos que , assim:
Ou seja,
Passo 4
Agora é só substituirmos o valor que encontramos:
Logo, mostramos que
É verdade
Resposta
Ei, a resposta está no passo a passo :)